Hvis puslerierne driller, så er der hjælp at hente i matematikken længere nede på siden.
1. udfordring
Tegn en konvolut som den på billedet på et stykke papir med én lang streg – det vil sige, at når du først er startet må du ikke løfte blyanten, før du er færdig. Det er ikke tilladt at tegne den samme streg to eller flere gange. Hvis det ikke lykkedes i første forsøg, så prøv igen, det kan lade sig gøre uden snyd.
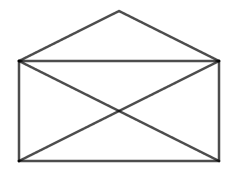
2. udfordring
Hvilke af disse figurer kan ikke tegnes med en lang streg?
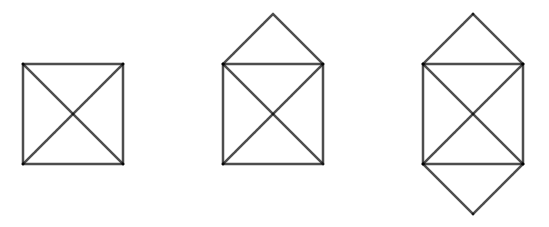
3. udfordring
Kan det lade sig gøre at tegne en lang streg gennem alle 16 vægge i denne figur, således at alle væggene krydses præcis en gang? Du bestemmer selv hvor stregen starter og slutter.
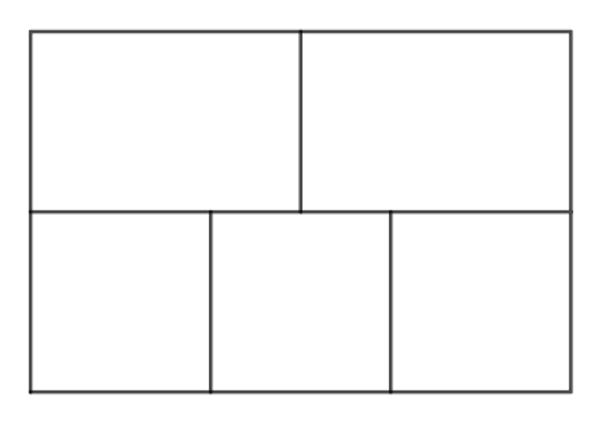
Få hjælp af matematikken: Grafteori
Måske kendte du allerede tegneopgaven i 1. udfordring, hvor det gælder om at tegne en konvolut som den på billedet med én lang streg – og måske kender du endda også en løsning med to helt bestemte start- og sluthjørner, men ved du hvorfor det lige er de hjørner, der virker? Det kan matematik hjælpe dig med at svare på.
Hints til udfordringerne?
Tegn en konvolut som den på billedet på et stykke papir med én lang streg – det vil sige, at når du først er startet må du ikke løfte blyanten, før du er færdig. Det er ikke tilladt at tegne den samme streg to eller flere gange.
Kan du løse opgaven? Hvis du ikke har forsøgt, så gør lige et enkelt forsøg inden du læser videre.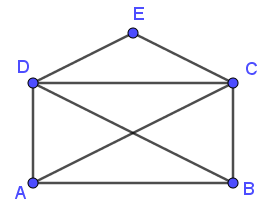
To af punkterne er gode at starte i og med de tre andre går det galt hver gang, men hvilke og hvorfor?
Lad os først overveje udfordringen. Vi skal tegne konvolutten med én streg uden at løfte blyanten. Vi har altså kun én enkelt streg at gøre godt med. Sådan en streg kan se ud på uendelig mange måder, men uanset hvad, så har stregen præcis to ender – en hvor du starter og en hvor du slutter. Hvis du starter og slutter præcis det samme sted, er det dog ikke rigtig til at se de to ender.
Sådan må det altså også være med løsning på vores konvolutudfordring – stregen har præcis to ender!
Lad os kigge nærmere på hjørnerne (A, B, C, D og E) på konvolutten. De er alle en slags knudepunkter for den lange streg, stregen skal gå fra et knudepunkt til det næste og fortsætte sådan indtil hele konvolutten er tegnet. De korte streger mellem knudepunkterne kalder vi for kanter. Fx er der en kant mellem punkterne B og D, men der er ikke en kant mellem punkterne A og E.
Når stregen kun har to ender, så må mindst tre af de fem knudepunkter være nogle, hvor stregen kun kommer forbi, disse punkter er hverken start- eller slutpunkt.
Lad os forestille os sådan et punkt, hvor stregen hverken starter eller slutter. Stregen kommer hen til punktet og fortsætter videre, der er nu to kanter ved punktet – en derhen og en væk. Kommer stregen forbi en gang mere er der nu fire kanter ved punktet. Og sådan vil det fortsætte med at der bliver lagt to kanter til for hver gang stregen kommer forbi punktet.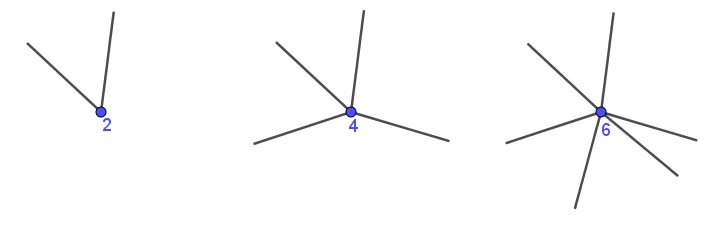
På den måde kan vi tælle antallet af kanter ved hvert at knudepunkterne. Dette tal kalder vi for knudepunktets valens. Knudepunkter, hvor stregen hverken starter eller slutter vil, som vi lige har fundet ud af ovenfor, altså altid have en valens, som er et lige tal – en lige valens.
I et knudepunkt, hvor stregen enten starter eller slutter vil til gengæld altid have en ulige valens. I de tilfælde hvor stregen både starter og slutter i samme knudepunkt vil må valensen blive lige – kan du forklare hvorfor?
Prøv at tælle valensen på knudepunkterne i konvolutten. Kan det hjælpe dig til at finde de to gode startpunkter?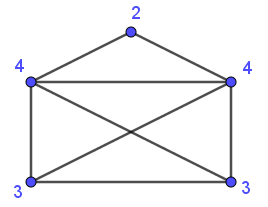 Der findes apps med spil, som er bygget op omkring ideen med en-stregs-tegninger. Hvis du søger på ”one touch drawing”, ”one line” eller lignende, så finder du flere forskellige.’
Der findes apps med spil, som er bygget op omkring ideen med en-stregs-tegninger. Hvis du søger på ”one touch drawing”, ”one line” eller lignende, så finder du flere forskellige.’
I en app’en One touch Drawing ser konvolutudfordringen sådan ud: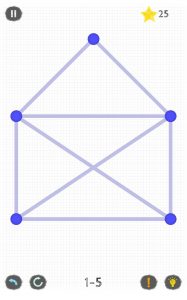
En anden app (1LINE) har denne variant: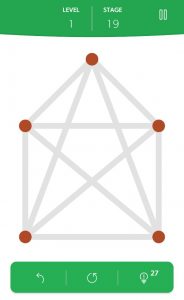
Links til apps:
One touch Drawing: iOS / Android
1LINE: iOS / Android
Kan du løse varianten? Hvis du bruger din viden om lige og ulige valens, hvilken af de to opgaver vil du så mene er nemmest?
Matematikken kan ikke kun bruges som hjælp til at finde en løsning, men også til at afgøre, om der overhovedet er en løsning. Her er tre næsten ens opgaver – den i midten er den kendte konvolutudfordring, men hvad med de to andre, er mulige at løse?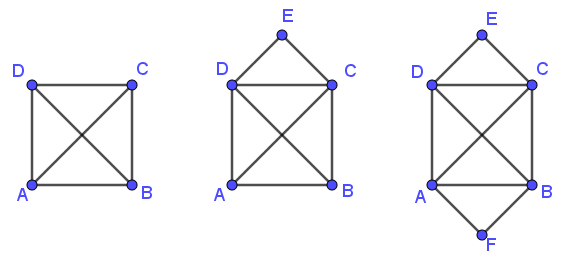
Den sidste udfordring er lidt anderledes, men kan du alligevel på en eller anden måde bruge din viden om valens til at løse den?
Er det muligt at tegne én lang streg således at alle væggene (16 styks) i figuren bliver krydset af stregen præcis en gang? Du må selv bestemme, hvor du vil starte og slutte.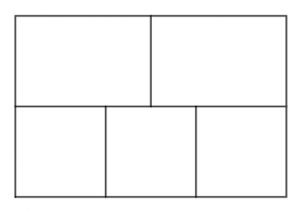 Her er et forsøg undervejs, men stregen mangler stadig at krydse en del af væggene.
Her er et forsøg undervejs, men stregen mangler stadig at krydse en del af væggene.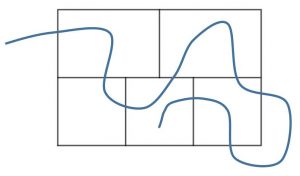
Ekstra udfordring:
Til allersidst et spørgsmål du måske kan svare på, hvis du bruger din viden om valens og hvor mange ender en streg har:
Avisen du læser er en del af et projekt MatKult, som er et samarbejde mellem fem institutioner og derfor kan vi godt lide femkantede figurer. En særlig femkantet figur er Petersen-grafen nedenfor. Den kan ikke tegnes med én lang streg. Hvor mange streger skal du mindst bruge? 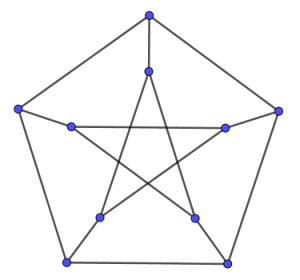

Start debatten med en kommentar