Har du nogensinde overvejet, hvorfor en klassisk fodbold egentlig ser ud, som den gør. Hvorfor består den af forskellige former? Er den matematisk set egentlig rund? Hvordan laver man noget rundt ud af noget fladt? Kunne den have set ud på en anden måde? Alt det og mere kan du måske blive klogere på i denne artikel.
De fleste kender sikker sportsgrenen fodbold, men ellers er der her en helt kort forklaring. Fodbold er en sport for to hold med 11 spillere på hvert hold. Lidt forsimplet så spilles en særlig bold rundt mellem spillerne og hvert hold kæmper om, at få bolden flest gange ind i modstanderens mål. Hvert hold har udpeget en målmand, som i nogle tilfælde må røre bolden med hænderne alle andre må kun spille med fødderne. Sporten kræver ikke ret meget andet udstyr end en fodbold, hvilket måske kan være årsag til, at det er en af de mest udbredte sportsgrene i hele verden.
Både Danmark og Tyskland har en lang fodboldtradition. Et af de danske højdepunkter var i 1992, hvor Danmark slog netop Tyskland i EM-finalen i Sverige med 2-0. Tyskland har dog stået øverst på podiet ved både EM og VM flere gange. Hele 3 gange har Tyskland fået EM-pokalen med hjem efter sejre på 3-0 over Sovjetunionen i 1972, på 2-1 over Belgien i 1980 og på 2-1 over Tjekkiet i 1996. Tyskland har også kunnet skrive verdensmestre på visitkortet hele 4 gange efter sejre over Ungarn i 1972 på 3-2, over Holland i 1980 på 2-1 og over Argentina i både 1990 og 2014, begge gange med sejre på 1-0. Den klassiske sorte og hvide fodbold, som denne artikel handler om, har været anvendt ved slutrunder igennem flere årtier. Den blev brugt første gang ved EM i 1968 og var for første gang official bold ved VM i 1970 i Mexico.
| Faktaboks |
|---|
| I en ligesidet figur (2D) er alle kanter (sider) præcis lige store og alle vinkler (hjørner) er ens. Et kvadrat er derfor et eksempel på netop en ligesidet figur. Femkanter kalder vi i matematikken for pentagoner. Vi kender ordet fra det amerikanske forsvarsministerium Pentagon, som har form som ikke blot en femkant, men faktisk en ligesidet femkant. Sekskanter kalder vi for hexagoner. Ligesidedede hexagoner kender vi fra bikuber der er bygget op af netop disse. |
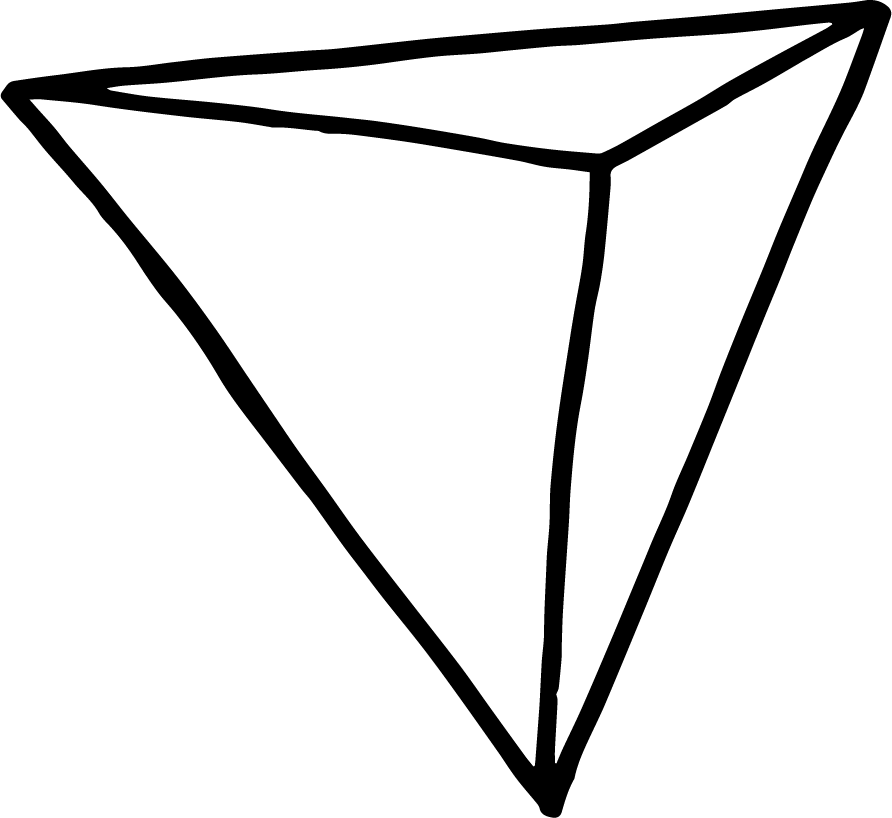
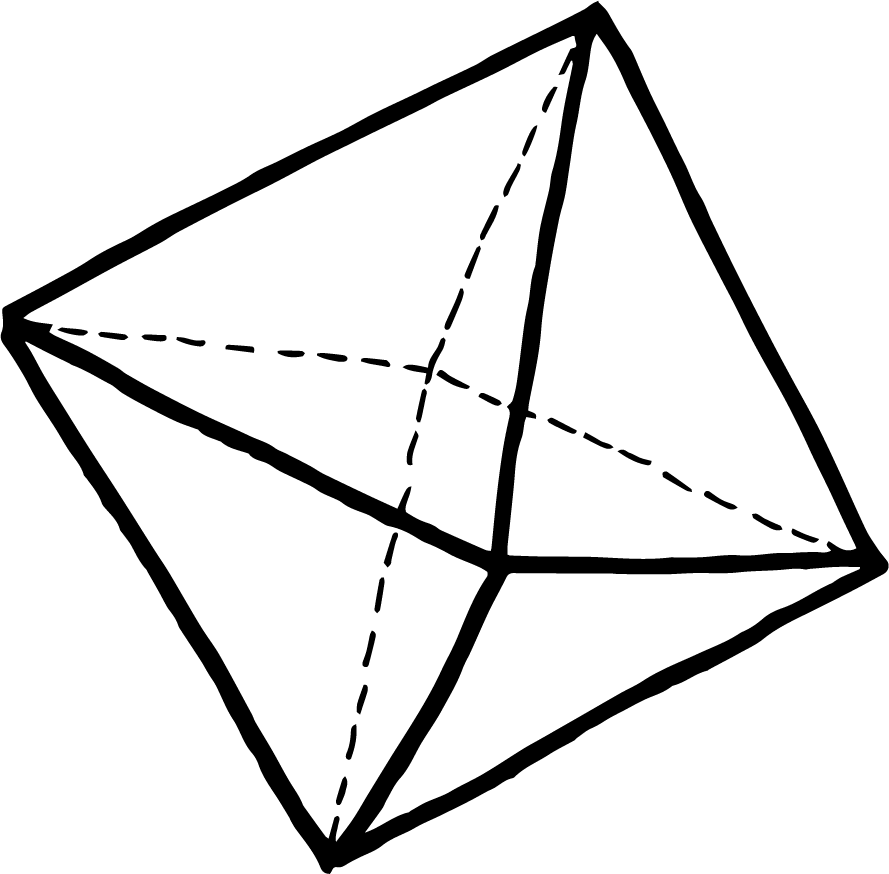

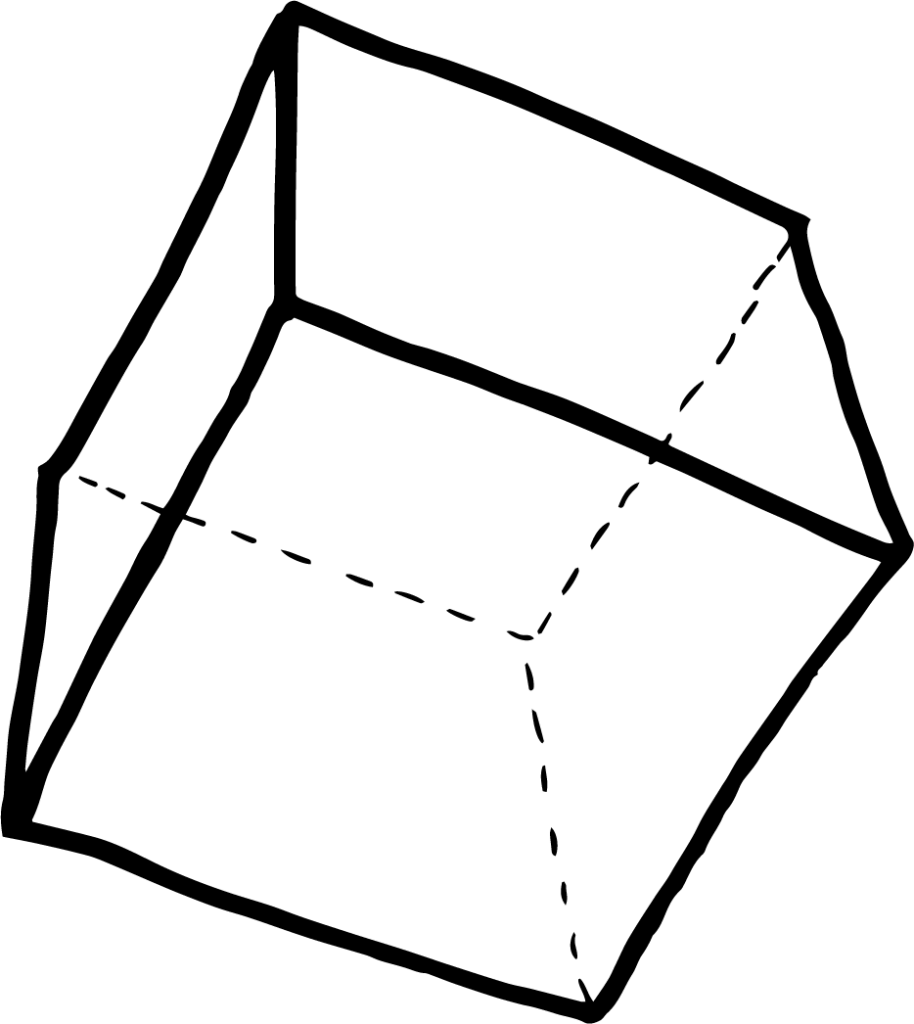

Hvis vi ønskede en lidt mere rund form, kunne vi forsøge at bygge bolden op som et ikosaeder, som består af 20 ligesidede trekanter der mødes 5 og 5 i 12 hjørner. En sådan rumlig figur, som det fremgår af billedet herover, vil gøre bolden mere rund, men stadig temmelig utilregnelig, da den stadig vil kunne hoppe og trille i alle retninger afhængig af, hvordan den lander.
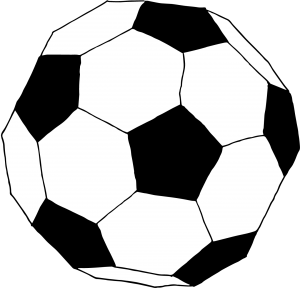
Hvis vi nu forestiller os, at vi skærer spidserne af i alle 12 hjørner, så vil den rumlige figur nu komme til at bestå af 12 ligesidet femkanter og 20 ligesidet sekskanter. Hvis vi nu farver femkanterne sorte og sekskanterne hvide, så ligner den, noget vi har set før. Det er nemlig sådan, at den klassiske fodbold er opbygget, men spørgsmålet er hvorfor?
Det fleste kan måske huske fra deres skoletid, at vinkelsummen i en trekant er 180 grader og vinkelsummen i en firkant er 360 grader, men hvordan forholder det sig i en femkant og i en sekskant? Ser vi på trekanten, så kan vi udføre et klassisk matematisk bevis for vinkelsummen i en trekant, men vi kan også overbevise os selv om, at det nok er rigtigt ved at udføre en masse undersøgelser af vilkårlige trekanter. Et bevis vil ikke blive fremført her, men vi tager udgangspunkt i, at vinkelsummen i en trekant er 180 grader. Det kan vi bruge til at finde vinkelsummen i en firkant, femkant, sekskant, ja faktisk i en hvilken som helst plan figur.
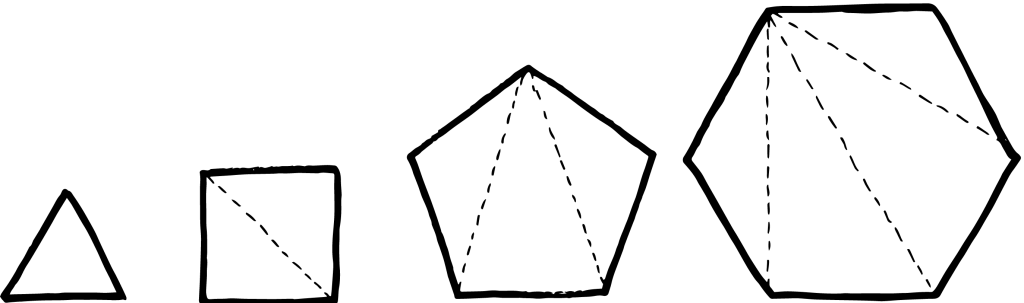
Som det ses herover, så vil en firkant kunne deles ved at tegne en diagonal fra et hjørne til et andet. På den måde kommer firkanten til at bestå af 2 trekanter. Da vinkelsummen i en trekant er 180 grader, så må vinkelsummen i 2 trekanter være 2×180 grader, altså i alt 360 grader. Femkanten kan ligeledes deles med en diagonal. Hermed får vi en trekant og en firkant. Firkanten deler vi igen, og femkanten består nu af 3 trekanter med en vinkelsum på 3×180 grader, altså 540 grader. Det samme kan vi gøre med sekskanten, som vil give en vinkelsum på 4×180 grader, som er lig 720 grader. På samme måde kunne vi fortsætte, hvorfor vinkelsummen i en hvilken som helst figur let kan findes ved at tælle antallet af hjørner og dermed det mindste antal trekanter, som figuren kan inddeles i.
I en ligesidet figur er alle hjørner ens, hvorfor vinklen i hjørnerne vil være den samme. Derfor vil hver vinkel i figurerne være vinkelsummen delt med antallet af vinkler. Hvorfor en vinkel i en ligesidet figur vil være lig med:
Trekant: 180 grader/3 = 60 grader
Firkant: 360 grader/4 = 90 grader
Femkant: 540 grader/5 = 108 grader
Sekskant: 720 grader/6 = 120 grader
Ser vi på de platoniske legemer, så har disse vinkelsummer betydning for hvor rund en bold bygget efter et af de platoniske legemer vil blive. For at bygge en rumlig figur, skal vi sætte mindst 3 figurer sammen i hvert hjørne. Sætter vi 4 trekanter sammen, som i tetraederet, så vil vinkelsummen i et hjørne, hvor 3 trekanter mødes, være 3*60 grader, altså 180 grader. Dette hjørne vil opleves som meget spidst.
Sætter vi en ekstra trekant ind, så ikke bare 3, men 4 trekanter mødes i et hjørne, som i et oktaeder, så vil vinkelsummen i et hjørne være 4*60 grader, altså 240 grader. Denne rummelige figur vil være mindre spids i hjørnerne.
Prøver vi nu at sætte en 5. trekant ind i hvert hjørne vil vi ende med at bygge et ikosaeder. Her vil vinkelsummen i hvert hjørne være lig 5*60 grader, altså 300 grader. Denne rummelige figur vil opleves endnu mindre spids i forhold til tetraederet og oktaederet.
Sætter vi en 6 trekant på, så vil vi opdage, hvorfor vi ikke kan bygge flere platoniske legemer af trekanter end de tre nævnte. Her vil vinkelsummen i et hjørne blive 6*60 grader, altså 360 grader, og hvorfor kan vi ikke bygge en rumlig figur? ”Tænke, tænke, tænke…”
Hjørnet vil blive helt fladt, og vi vil derfor aldrig kunne lave det til en rumlig figur. På samme måde kan vi, ved at kigge på kvadrater, pentagoner og heksagoner, argumentere for, hvorfor der ikke kan laves andre end de 5 nævnte platoniske legemer. Prøv at se, om du kan følge tankegangen.
Men hvad så med vinkelsummen i hjørnet på den klassiske fodbold? Et hvilket som helst hjørne i fodbolden vil bestå af et hjørne fra en femkant og to hjørner fra to sekskanter – tjek selv efter på billedet af fodbolden. Dette giver en samlet vinkelsum i hjørnet på 108 + 120 + 120 = 348 grader, som er relativt tæt på 360 grader, som vil gøre hjørnet helt fladt, men langt nok fra 360 grader til, at vi vil kan lave en rumlig figur. Som det fremgår af modellen, så vil den rummelige fodbold i matematisk forstand stadig have skarpe kanter, men da den er syet af et materiale, som kan give sig, så vil vi opleve fodbolden bestående af 12 ligesidet femkanter og 20 ligesidet sekskanter som rund, når den pustes op i et materiale som kan give sig, fx en læderbold. Dette er grunden til, at den klassisk sorte og hvide fodbold ser ud, som den gør.
Fodbolde kan faktisk også bygges op af andre af de platoniske legemer. Dette og andre sjove facts om fodbolde kan du finde her: https://www.youtube.com/watch?v=cwWBpjeyRS0, hvor Matt Parker, som er australsk matematiklærer og standupkomiker, forklarer geometrien bag forskellige fodbolde.
Det er også muligt, at læse lidt mere omkring boldens historie her: https://web.archive.org/web/20150702050750/http:/www.selectsportamerica.com/history/
Illustrationer: Helle Lykke Østerby – November 2020

Start debatten med en kommentar