 Det franske sæt spillekort, som de mest almindelige spillekort korrekt hedder, har fundet mange anvendelser gennem tiden. Sættet består af 52 spillekort opdelt i fire kulører (spar, hjerter, klør, ruder) med hver 13 kort. Det franske sæt spillekort kan spores tilbage til 1377 i Frankrig, hvortil idéen om spillekort kom fra Egypten. I middelalderens Frankrig repræsenterede kulørerne de fire stænder. Spar som står for sværdet, repræsenterede adelen, hjerter, som står for alterkalken, repræsenterede gejstligheden, ruder, som står for mønten, repræsenterede købmændene, og bønderne repræsenteres af klør, som står for hyrdestaven. Det franske sæt spillekort er det mest brugte i både Nordeuropa, Nordamerika, Afrika og Asien, men der findes også andre typer såsom det spanske, som bruges i Spanien og Sydamerika eller det tyske sæt, som anvendes mest i Sydtyskland. Spillekortene bliver brugt til flere ting, da man både kan benytte dem, når man er alene, og når man er i grupper. Kabaler er kortspil, hvor man som enkeltperson kan spille mod kortenes struktur for at få kabalen til at gå op i forskellige systemer, fx 7-kabale eller Urkabale. Hvis man er flere end en, findes der utallige kortspil, hvor man kan spille mod hinanden, og derudover har kortspil også fået en underholdningsdimension, hvor de bliver benyttet til at lave korttricks af bl.a. tryllekunstnere. Matematik spiller en stor rolle i mange af disse anvendelser af spillekort, og i seneste udgave af MatOnline fra januar beskrives ’matematisk magi i korttricks’ i artiklen af samme navn. I denne artikel kigger vi nærmere på, hvordan matematikken kommer til udtryk i forskellige kortspil, hvor man bruger det franske sæt spillekort, og vi ser på, hvordan aftenhyggen hjemme i familierne kan være med til at styrke ens matematiske kunnen og matematiske overblik.
Det franske sæt spillekort, som de mest almindelige spillekort korrekt hedder, har fundet mange anvendelser gennem tiden. Sættet består af 52 spillekort opdelt i fire kulører (spar, hjerter, klør, ruder) med hver 13 kort. Det franske sæt spillekort kan spores tilbage til 1377 i Frankrig, hvortil idéen om spillekort kom fra Egypten. I middelalderens Frankrig repræsenterede kulørerne de fire stænder. Spar som står for sværdet, repræsenterede adelen, hjerter, som står for alterkalken, repræsenterede gejstligheden, ruder, som står for mønten, repræsenterede købmændene, og bønderne repræsenteres af klør, som står for hyrdestaven. Det franske sæt spillekort er det mest brugte i både Nordeuropa, Nordamerika, Afrika og Asien, men der findes også andre typer såsom det spanske, som bruges i Spanien og Sydamerika eller det tyske sæt, som anvendes mest i Sydtyskland. Spillekortene bliver brugt til flere ting, da man både kan benytte dem, når man er alene, og når man er i grupper. Kabaler er kortspil, hvor man som enkeltperson kan spille mod kortenes struktur for at få kabalen til at gå op i forskellige systemer, fx 7-kabale eller Urkabale. Hvis man er flere end en, findes der utallige kortspil, hvor man kan spille mod hinanden, og derudover har kortspil også fået en underholdningsdimension, hvor de bliver benyttet til at lave korttricks af bl.a. tryllekunstnere. Matematik spiller en stor rolle i mange af disse anvendelser af spillekort, og i seneste udgave af MatOnline fra januar beskrives ’matematisk magi i korttricks’ i artiklen af samme navn. I denne artikel kigger vi nærmere på, hvordan matematikken kommer til udtryk i forskellige kortspil, hvor man bruger det franske sæt spillekort, og vi ser på, hvordan aftenhyggen hjemme i familierne kan være med til at styrke ens matematiske kunnen og matematiske overblik.
Kortspils matematiske egenskaber
Kortspil kan fremme og forstærke matematisk tankegang, hvilket bl.a. benyttes i skoler. Gennem leg kan man introducere børnene til en langvarig og vidtgående kulturel praksis. I starten lærer de kortenes overordnede struktur at kende for senere at kunne indgå i kortspil, som kræver et større overblik og rationel tankegang. Kortspillene kombinerer spillekortenes fuldstændige enkelhed med en ubegrænset alsidighed i kortspillenes reglement. Det betyder, at alsidigheden ligger i enkelheden, hvilket er baseret på matematiske principper. Det betyder, at ligegyldigt om det er et basalt eller et komplekst kortspil, så styrker det de matematiske ræsonnementer. Kombineret med kortspils afhængighed af held i form af tilfældigheden i, hvilket kort man trækker, kan børn opleve en motiverende kraft i at engagere sig i kortspillet og fremme deres matematiske evner. Kortspils betydning for børns læring er også et element, som har interesseret forskere rundt om i verdenen for at undersøge betydningen og effekten hos både små børn og lidt ældre. Herunder vil to kortspil blive gennemgået, og det vil blive præsenteret, hvilke matematiske principper, som kommer i spil i hvert af dem.
Krig
Det første kortspil, som præsenteres, er Krig, som er et af de mere basale kortspil, som vil være mest anvendeligt for børnehavebørn, og når man skal lære matematik for første gang. Man spiller typisk en mod en, og man benytter hele dækket på 52 kort. Dækket deles tilfældigt ud til deltagerne, så de har en bunke kort foran sig med bagsiden opad. Samtidig trækker begge spillere det øverste kort fra hver deres bunke, og den, som har det kort med den højeste værdi, vinder sættet. Dette bliver ved, indtil man ikke har flere kort i sin bunke, hvorefter man tager de sæt, som man har vundet, blander og benytter igen. Vinderen er den, som til sidst har vundet alle kortene fra modstanderen. I de tilfælde, hvor begge spillere trækker et kort med den samme værdi, er der KRIG, og begge spillere lægger yderligere tre kort ud foran sig med bagsiden opad. Begge spillere vælger på samme tid et af de tre kort, og den med den højeste værdi vinder alle kortene, som er med i krig-runden. Dette spil er meget basalt, men giver samtidig mange muligheder for varianter, som kan gøre spillet lidt mere avanceret. Eksempler på dette kan være, at i krig-runden vender man alle tre kort, og den spiller, som har den største sum, difference eller produkt vinder krigen. Spillets grundregler giver mulighed for, at deltagerne selv kan påvirke spillets regler.
Når spørgsmålet går på hvilken matematisk magi, der ligger gemt i dette kortspil, er der flere ting, som kommer til udtryk. Helt grundlæggende arbejdes der med at tælle hvor mange kort, man deler ud, og når man har krigsrunden, skal man trække tre kort frem. Herudover arbejdes der også med sammenligning af værdierne af kortene. Dette gælder både med hensyn til, hvilke tal på talkortene mellem 2 og 10, der er størst; men også værdien af kortene bonde, dame, konge og es. Dette inkluderer også princippet i, at to kort kan være lig med hinanden, selvom det ikke er det samme kort, men de har samme værdi. Disse matematiske principper vil passe godt med børnehaven, men hvis man arbejder med modifikationer af spillet, kan man styrke ekstra ting som additionsstykker, hvor de skal finde den største sum, subtraktionsstykker, hvor de skal finde den største difference eller multiplikationsstykker, hvor man skal finde det største produkt i krigsrunden.
24
Et andet kortspil, hvor der arbejdes med lidt mere udfordrende matematik, er 24. Spillets grundprincip går ud på, at 2-4 personer spiller mod hinanden kun med brug af kortene fra es til 10 i alle fire kulører. Spillet er egnet til børn i 4.-7. klasse. Man spiller ved, at der deles fire kort ud til hver deltager. Opgaven er nu at lave et regnestykke ved brug af de fire regnearter og alle de fire kort, man har fået givet, og resultatet skal være så tæt som muligt på 24. Den, som får lavet det regnestykke, hvis resultat er tættest på 24, får et point, og vinderen af spillet er den, som først får det antal point, man på forhånd har aftalt. Der er flere muligheder for at ændre dette spil. Man kan ændre værdien af regnestykket, så det ikke er 24, det skal give hver gang, eller man kan inkludere andre matematiske operationer som rødder og eksponenter. Ved en anden variant af spillet får hver deltager alle kortene i en kulør, og så skal de se hvor mange regnestykker med resultatet 24, de kan lave ved brug af fire kort. Den spiller, som kan lave flest forskellige regnestykker, vinder. 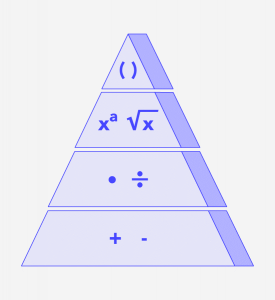
Det åbenlyse, som man her arbejder med matematisk, er de fire regningsarter, men på grund af det mange antal gentagelser der er i dette spil, får deltagerne mulighed for hele tiden at blive mindet om, hvordan man arbejder med matematisk algebra, ligesom regnehierarkiet også får en stor betydning for opstillingen af regnestykkerne, som skal give 24. Ved tilføjelsen af rødder og eksponenter er der en ekstra dimension, man skal tage højde for. Det algebraiske ræsonnement, man skal udføre, kræver en stor grad af mental matematiktænkning, som er ens evne til at lave udregninger i hovedet uden at have papir og blyant ved sig. Den mentale matematiktænkning er den egenskab, der gør, at man kan lave overslagsregning, og den kan også styrke ens tidsfornemmelse, så man kan forstå tiden uden at skulle udregne tidspunkter hele tiden, men blot kan se tiden for sig i hovedet.
Matematikkens magi
Her er der præsenteret et par forskellige kortspil, som man kan spille og have det sjovt og hyggeligt med samtidig med, at man træner sin matematiske kunnen og ræsonnement. Denne effekt er brugbar for alle, som deltager i spillet. Børnene kan træne bl.a. de fire regningsarter og den mentale matematik, mens de voksne kan styrke det mentale ræsonnement, samtidig med at de kan vurdere effekten af kortspillet på børnenes kunnen. Hver familie eller gruppe har deres kortspil, som de spiller meget, og udfordringen for jer ligger nu i at gøre jer nogle overvejelser over hvilke dele af matematikken, der ligger i lige netop de spil, som I spiller. For det kan godt være, det ikke er helt så nemt at se som i eksemplerne i denne artikel, men i ethvert kortspil ligger matematikkens magi gemt, og selvom man ikke er klar over det, styrker det ens matematiske ræsonnement, men det bliver kun sjovere, hvis man også selv er klar over, hvad man bliver bedre til.
Hvis du synes, denne artikel har været interessant, så læs også MatOnline’s artikel: ”Matematisk magi i korttricks”, der gennemgår hvordan matematikken træder i kraft i en anden af kortspillets anvendelser; nemlig korttricks.

Start debatten med en kommentar