En af de mest udbredte naturvidenskabelige modeller er normalfordeling, der blev introduceret omkring 1730 af matematikeren Abraham de Moivre (1667-1754). Normalfordelingen beskriver en teoretisk ideel fordeling af en række observationers værdier og anvendes til at beskrive, hvordan et stort antal observationer, fx af højden eller vægten af hver enkelt person i en stor og ensartet gruppe, fordeler sig (spredning) omkring deres gennemsnit (middelværdi). Har man f.eks. målt 1000 personers højde og ser på, hvordan disse højder fordeler sig, så vil man ofte se, at størstedelen af observationerne ligger samlet omkring et gennemsnit, og at der så vil være færre og færre observationer, jo længe fra gennemsnittet man kommer. Normalfordelingen passer godt til sit navn, da den viser en fordeling af måleresultater, som i mange sammenhænge optræder naturligt, når man ønsker at beskrive et givet fænomen. Det kan fx være sandsynligheden for at få “krone” et bestemt antal gange ved mange møntkast. Ved 100 kast er det mest sandsynligt at få krone 50 gange, men alt mellem 40 og 60 er ikke usædvanligt, mens 0 gange er nærmest utænkeligt. Modellen repræsenteres ofte grafisk ved hjælp af den såkaldte klokkeformede kurve eller ”The Bell Curve”, hvor toppunktet af kurven angiver middelværdien af det statistiske materiale, og bredden af kurven er et mål for, hvordan observationerne fordeler sig, også kaldet spredningen eller standardafvigelsen.
Nutidig sandsynlighedsregning og statistik er bundet op på Gauss’ normalfordeling, som derfor bliver brugt i utallige sammenhænge. Fx når man skal korrigere for de atmosfæriske forstyrrelser, der påvirker signalerne ved trådløs kommunikation i forbindelse med fx mobiltelefoni og transmission af tv og radio. Summen af disse tilfældige og naturligt forekommende påvirkninger af signalerne er normalfordelt. Normalfordeling bruges også i medicinalindustrien i forbindelse med dokumentation af ny medicin. Her ønsker man typisk at beregne usikkerheden på den gennemsnitlige effekt af medicinen, hvilket ofte involverer beregninger af normalfordelingen.
Anvendelsen af normalfordelingen er udbredt, men også i nogle tilfælde kontroversiel. Således udgav to amerikanere, psykologen Richard J. Herrnstein og politologen Charles Murray, i 1964 bogen ”The Bell Curve”, hvor en af hovedpointerne er, at der er korrelation mellem intelligens målt med intelligenskvotient (IQ) og sociale variabler som fx indkomst, beskæftigelse og kriminalitet. Forfatterne argumenterer for, at en persons IQ derfor er bedre til at forudsige sociale variable end forældrenes sociale og økonomiske baggrund og uddannelsesniveau. Bogen førte bl.a. til en debat om, hvorvidt forskelle i IQ har genetisk oprindelse, hvilket ledte til forslag om at begrænse indvandring og fattige kvinders ret til at få børn.
Der er desværre i historien mange eksempler på, hvordan matematik misbruges til at understøtte etniske og sociale fordomme, fx i forbindelse med køn, race og gener og racisme. Derfor er en kritisk tilgang til anvendelsen af matematiske grafer selvfølgelig vigtig, men ligeså vigtigt er det, at vi er i stand til at uddrage og konstruktive anvende den ofte omfattende videnskabelige information en graf indeholder. Som den kendte tyske sociolog Ulrich Beck skrev i sit hovedværk ”Risikosamfundet”, så er en videnskabelig rationalitet uden en samfundsmæssig rationalitet tom, ligesom en samfundsmæssig rationalitet uden en videnskabelig rationalitet er tom. Således er der det paradoks, at matematikken dels tilstræber at give en objektiv forklaring på generelle fænomener og processer i naturen og samfundet, dels er værdiladet, når den bringes i spil på et samfundsmæssigt plan.
Lad os nu se på hvordan tolkning af grafer kan have betydning for vores opfattelse og forståelse af menneskelig diversitet og ensartethed. Nedenfor ser vi normalfordelingskurver for to populationer af mennesker. Hvad kurverne viser om de to populationer er for vores pointe underordnet, men det kunne fx være fordelingen af gener i henholdsvis en europæisk og en afrikansk population.
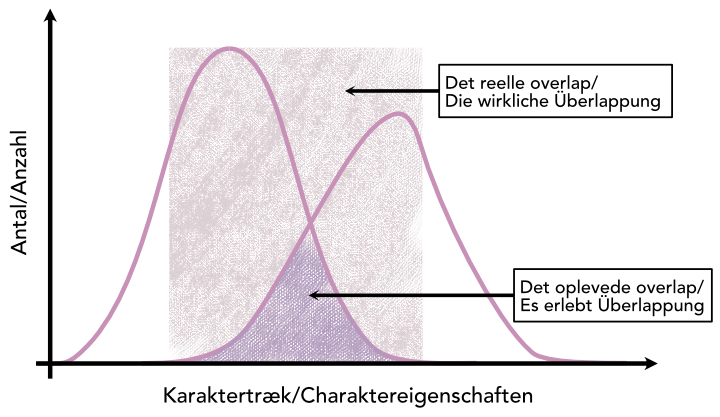
Man vil nok umiddelbart fortolke, at det trekantslignende område mellem de to kurver repræsenterer det, de to populationer har til fælles. Den fortolkning understreger forskelle i populationerne og leder til en opfattelse af, at de to populationer kun har meget lidt tilfælles. Det reelle overlap mellem de to populationer er imidlertid området, hvor de to kurver har fælles værdier på første aksen. Dette område er langt større end det trekantlignende område og indeholder begge populationers median, der er den midterste værdi i et ordnet sæt af observationer. Værdierne af medianer giver således ingen informationer om individerne i de to populationer, som fx race eller andre former for opdeling af populationerne. En graf kan således ikke anvendes uden en kritisk analyse, både i forhold til dens egen brugbarhed og relevans og i forhold til at kommunikere med andre om grafen og dens resultater.

Start debatten med en kommentar