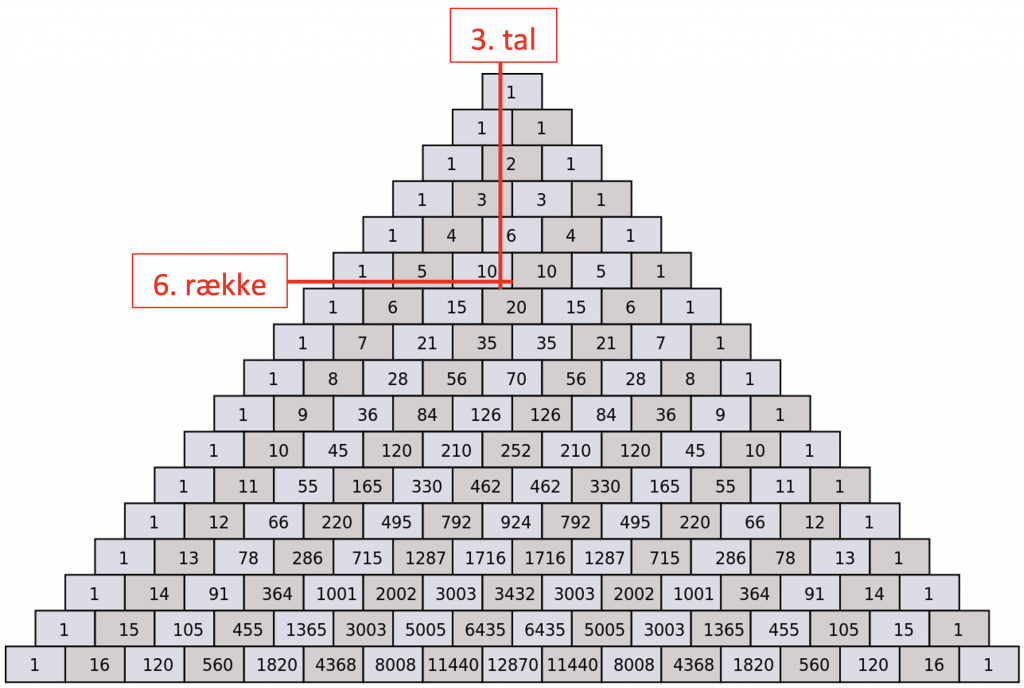
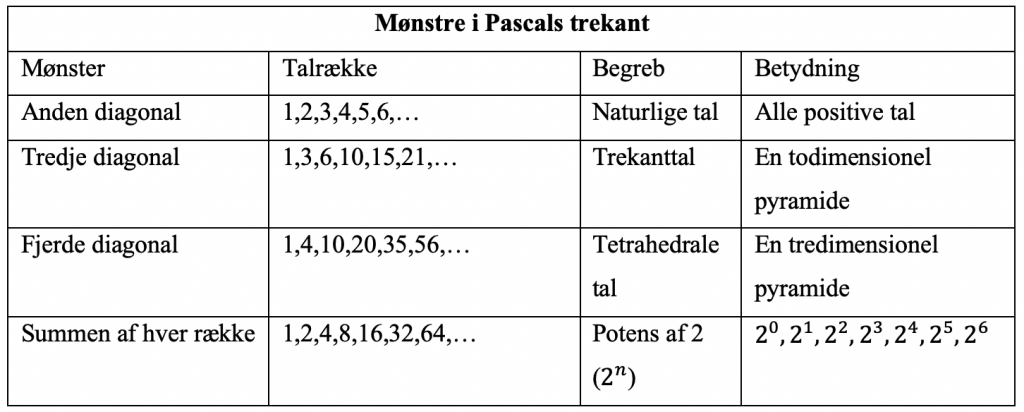
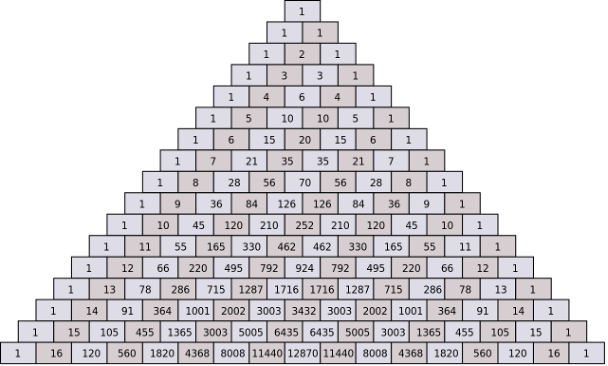
Den første sommerdag nærmer sig, og issæsonen er begyndt. For mange er det lig med en gammeldags isvaffel. Men favoritisboden har hele 10 forskellige kugler at vælge imellem, og du kan ikke beslutte dig for hvilken kombination, du har lyst til, når du skal have din is med to kugler. Så melder spørgsmålet sig. Hvor mange gange i løbet af sommeren skal du besøge isboden, før du kan prøve alle kugler i alle kombinationer? Det har vaffelsælgeren aldrig lige tænkt over, så han kan desværre ikke hjælpe dig. Du kan godt regne ud at der må være en matematisk måde at regne det ud, men det ville være nemmere, hvis man bare kunne slå det op, uden man skal lave en længere matematisk beregning. Til det kan det matematiske koncept ”Pascals trekant” benyttes. Pascals trekant er kort fortalt en pyramide, hvor der på det øverste trin er en mursten med tallet et. I rækken under er der to mursten begge med tallet et. I den næste række er der tre mursten med henholdsvis tallene en, to, en på dem. Tallet på murstenen bliver beregnet ved at man lægger de tal sammen som mursten har kontakt med fra den ovenstående række. Dette er vist på nedenstående illustration ligesom man kan se sådan en pyramide med 17 rækker:
Trekantens oprindelse og anvendelse
Inden vi ser hvordan denne specielle pyramide kan hjælpe dig med isproblemet, vil vi se på trekantens oprindelse og nogle af de matematiske hemmeligheder den gemmer på. Pascals trekant blev udformet af den franske matematiker og fysiker Blaise Pascal, som levede fra 1623-1662. I sin korte levetid formåede Pascal at præsentere flere store opdagelser inden for både matematik og fysik, hvor han i dag mest er kendt for enheden for tryk (Pascal), som han lægger navn til. Udover sit arbejde med tryk i hovedsageligt væsker udførte han også et pionerarbejde indenfor sandsynlighedsregningen, og han ligeså opfandt den første regnemaskine. I sit arbejde med sandsynlighedsregningen blev der posthumt i 1665 udgivet et værk ”Traité du triangle arithmetique”, som beskriver Pascals trekant. Udover at være gennembrydende i den forstand, at det var den første gang matematisk induktion[1] blev benyttet gav trekantens udformning også grobund for mange andre matematiske teorier. Den angiver bl.a. koefficienterne, når man beregner kvadrat og kubiksætninger som ses nedenunder.
[1] Matematisk induktion dækker over det matematiske begreb som kan sidestilles med dominoeffekten. Der er et basisskridt hvor den første dominobrik vælter og et induktionsskridt hvor den næste brik vælter når den første er væltet. Dermed vil alle brikkerne i rækken vælte.
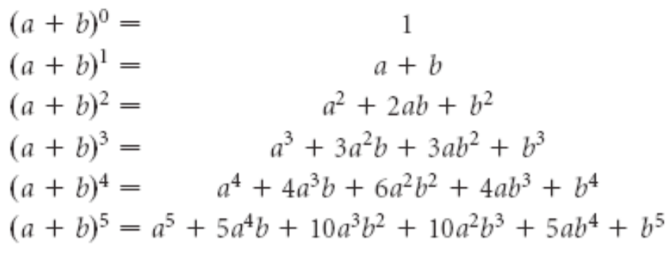
Selve konstruktionen af trekanten er nem, da det kun kræver at man lægger to tal sammen, men den kan visualisere adskillige matematiske begreber, som er langt mere avanceret end blot at lægge tal sammen. Nogle af de begreber vil blive præsenteret her. Først og fremmest så er alle mursten i trekanten binomialkoefficienter, og det er her sammenkædningen med sandsynlighedsregningen opstår.
Binomialkoefficienter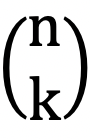 
angiver antallet af måder hvorpå man kan udtage ”k” forskellige elementer fra en pulje med ”n” forskellige elementer. Illustreret med Pascals trekant angiver ”n” nummeret på rækken startende fra nul. Dvs. den første række har nummer n = 0, den næste n = 1 osv. ”k” angiver tallene fra venstre mod højre også startende fra 0 og op. Ideen med trekanten er dermed, at værdien for en binomialkoefficient kan findes ved at undersøge den mursten, som stemmer overens med ”n” og ”k”-værdien fra koefficienten. Lad os prøve at se på et eksempel. Værdien 
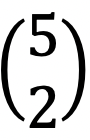kan man bestemme ved at finde den række, som har n = 5, hvilket vil være sjette række, da første række er den nulte række, og så skal man finde det tal i rækken, som har k = 2, som vil være det tredje tal fra venstre, da igen det første tal er k = 0 . Hvis man gør det på trekanten på billedet, vil man finde en mursten med tallet 10. For at bekræfte om dette er korrekt, kan man bruge den matematiske formel fra tabellen:
Dermed kan det ses, at teorien stemmer overens. Dette gælder for alle værdier i Pascals trekant. Konstruktionen af trekanten sagde, at en murstens værdi er de to ovenstående murstens værdier lagt sammen hvilket også kan udtrykket med binomialkoefficienter som man kan se i tabellen.
Denne struktur kan benyttes til flere aspekter indenfor matematikken. Dette illustrerer et Galtonbræt. Det er et bræt som vist her på billedet med en antal søm, som kugler kan løbe ned igennem. Ved hvert søm kan en kugle enten bevæge sig til venstre eller til højre for sømmet og bevæge sig ned gennem brættet for til sidst at lægge sig i en af kolonerne i bunden af brættet.
Selvom det teoretisk er tilfældigt om kuglen bevæger sig til venstre eller højre for hvert søm, vil man kunne sige noget om det mønster, som viser sig, når et stort antal kugler har bevæget sig ned gennem brættet. På det højre billede er der indtegnet en blå linje, som viser fordelingen hvorved kuglerne har lagt sig. Denne fordeling kaldes binomialfordeling og har en forbindelse med Pascal trekant. Hvis man tager en række i Pascal trekant og lader hver boks illustrere en kolonne og lader tallet i boksen illustrere antallet af kugler i den givne kolonne, så vil man kunne se den samme binomialfordeling, som der ses på Galtonbrættet. Dette er blot et af mange eksempler på hvordan Pascals trekant trækker tråde til matematikken.
For at vende tilbage til situationen med isbutikken, har vi et redskab til at finde frem til hvor mange gange man skal besøge boden i løbet af sommeren for at kunne smage alle kombinationer af kugler i ens isvaffel. Hvis ”n” angav antallet af forskellige elementer at vælge imellem, må det være 10, da der var 10 forskellige smage. Det betyder, vi skal finde rækken med i Pascals trekant, og ”k” angav antallet af forskellige smage med valgte, hvilket var 2. Det betyder, vi skal kigge på række 11 i trekanten og finde det 3. tal fra venstre, og dermed ved vi det antal gange vi skal besøge isbutikken. Efter et hurtigt kig i Pascals trekant fås tallet til 45, og vi kan dermed konkludere, det bliver en god sommer med masser af isvafler.
Gemte mønstre i trekanten
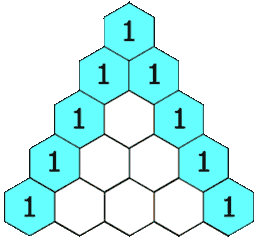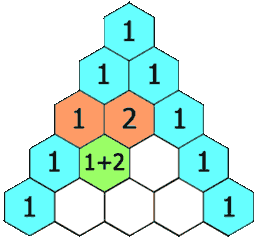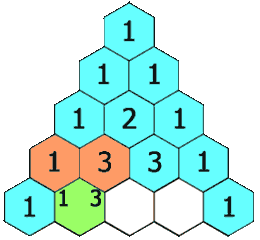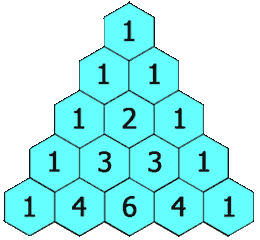
Denne matematik beskriver konstruktionen af Pascals trekant, og hvad man bl.a. kan bruge den til, men der gemmer sig rigtig mange andre matematiske begreber i trekanten. Ved første øjekast vil man hurtigt se at trekanten er symmetrisk, og hvis man kigger på diagonalerne fra toppen og ned, vil man kunne se en serie af tal. For eksempel den anden diagonal har talrækken 1, 2, 3, 4, 5, 6, …, som man vil kende som de naturlige tal. Men hvilke talrækker kan man se, hvis man kigger på den tredje og den fjerde diagonal? Et andet element, man kan overveje, er, om der er et mønster i summen af tallene i hver række. Prøv at overveje disse ting og tjek i tabellen nedenfor, om du har ramt rigtigt og se desuden også andre eksempler på gemte mønstre i Pascals trekant, som man vil kunne udforske.
Pascals trekant fortæller en historie om, at den selvom den i sin enkelthed er meget nem at konstruere, gemmer på store mængder af videnskab, som anvendes i mange forskellige områder såsom sandsynlighedsregning i matematikken, spektroskopi i kemiens verden og genbestemmelse i biologi.
Start debatten med en kommentar