Mange mennesker bygger deres hverdag op omkring struktur. Forskellige strukturer som kan gøre deres liv lettere. Det kan være, at man laver huskelister, eller man tænker i bokse for at adskille forskellige situationer. I matematikken arbejder man med begrebet kombinatorik, som medvirker som en ramme for strukturer. Det drejer sig om sammensætninger. Hvor mange måder kan man sætte objekter sammen og få forskellige muligheder. Det store spørgsmål omkring dette er, om den rækkefølge, som man udtager objekterne, betyder noget. Det spørgsmål tager kombinatorik op. Hvis man er på en restaurant og skal have en treretters menu, får man et menukort, hvor der er et bestemt antal forretter, hovedretter og deserter. I dette tilfælde er det nemt at bestemme, hvor mange mulige sammensætninger der er. Det gøres således:
[Antal af forretter] · [Antal af hovedretter] · [Antal af deserter]
=
[Antal muligheder for valg]
Ikke alle situationer er så nemme, så derfor er forskellige situationer beskrevet for at afhjælpe de problematikker.
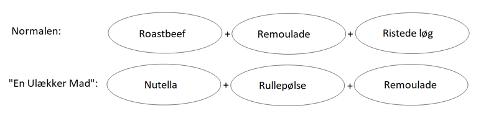
Hvis man belyser et eksempel, hvor man laver en rugbrødsmad, er normalen, at der er noget pålæg, som passer sammen og i en bestemt rækkefølge. På en roastbeefmad har man rækkefølgen roastbeef, remoulade og ristede løg, og på en leverpostejmad har man enten agurk eller rødbeder ovenpå leverpostejen. Det samlede antal af forskellige rugbrødsmadder er styret af en bestemt rækkefølge og sammensætning, som vi er opfostret med. Det betyder, at man kan sammensætte forskellige sammensætninger da ordenen har betydning i rækkefølgen. Denne opfattelse, af hvordan man lavede en rugbrødsmad, blev lavet om, da den danske DR-vært Sebastian Klein i 2001 debuterede med sekvensen ”En ulækker mad” i børneprogrammet ”Anton, min hemmelige ven”, hvor alle regler om rugbrødsmadder blev lagt på hylden, og man kunne sammensætte maden, som man havde lyst til, hvilket kunne blive til en mad med leverpostej, ost og roastbeef som for eksempel. Nu var maden ikke længere styret af en bestemt ordning, men kun hvilke muligheder der er foran dig altså en udvælgelse.
Kombination og permutation
De to ord; udvælgelse og ordning er essentielle for kombinatorikken, da det samlede antal af muligheder altid vil være større, hvis ordningen har betydning for dine valg. Metoden til at finde det samlede antal muligheder er forskellig for de to situationer. Derfor deles de to situationer op i kombinationer og permutationer. Kombination har samme betydning som udvælgelse, så en kombination er en måde at udvælge et bestemt antal fra en samlet gruppe uden at man tillægger rækkefølgen nogen betydning. Permutation betyder ordning og er de sammensætninger hvor rækkefølgen for udvælgelsen har betydning.

Spørgsmålet om hvordan man så i praksis beregner det samlede antal muligheder løfter sig nu. Ved et eksempel hvorved man skal udvælge fagkombinationer af tre ud fra ni forskellige fag, vil betydningen af rækkefølgen ikke have nogen indflydelse. Man vil til det første valg have ni muligheder. Til det næste vil der være otte forskellige muligheder og til det sidste valg vil der være 7 forskellige muligheder. Det bringer os frem til regnestykket 9 · 8 · 7 = 504 muligheder af fagkombinationer på sammen måde som ved eksemplet med den treretters menu. Det giver samlet rigtig mange muligheder, men vil de alle sammen være forskellige? Det vil de ikke, da vi hurtigt ser, at kombinationen der hedder fransk, tysk og engelsk er den samme som tysk, fransk og engelsk, da vi havde sagt at rækkefølgen ikke havde nogen betydning. Vi skal derfra have fjernet alle de gengangere, der er i de 504 muligheder. Dette kan man gøre ved at bestemme, hvor mange gange en enkel mulighed går igen. Hvor mange måder kan vi bytte rundt på de tre muligheder? Første fag kan være tre forskellige muligheder. Hvis man vælger en af dem, er der to muligheder for fag nummer to og igen én mulighed for fag nummer tre, hvilket giver 3 · 2 · 1 = 6. Så den samme kombination går igen seks gange blandt de 504 muligheder. Hvilket giver os regnestykket (9 · 8 · 7)/(3 · 2 · 1) = 84. Der er dermed 84 forskellige muligheder for at udvælge fagkombinationer af tre ud fra ni forskellige fag. Hvis man ser på det mere generelt får vi at dette er det samme som udregningen 9!/(3! · 6!), hvor ! angiver et tals fakultet. For at finde dette ganger man alle tal under det givne tal og sig selv sammen så 9! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9. Det betyder at de to vigtige observationer i dette eksempel er antal forskellige objekter her fag og antallet der udtages. Dermed ville man kunne bestemme antallet af forskellige kombinationer, i situationer hvor der er rigtig mange forskellige objekter at vælge imellem.
Når ordningen for ens udvælgelse har betydning, beskæftiger man med antallet af permutationer. Dette vil samlet set give et større antal af muligheder. Hvis man igen ser på antallet af muligheder for fagkombinationer ud fra ni fag, hvor rækkefølgen har betydning. Rækkefølgen kan have betydning, hvis man skal fordele sin tid ud fra hvilke fag, man udvælger først, får vi følgende muligheder som før: 9 · 8 · 7 = 504, men da ordenen har en betydning, kan vi ikke bare fjerne de muligheder hvor fagene er byttet rundt på pladserne. Vi får dermed udregningen 9!/6! = 504. Der er dermed 504 forskellige permutationer. Det giver samlet set væsentlig flere muligheder end i situationen, hvor ordningen ikke havde nogen betydning.

Hvis man studerer børneprogrammet med Sebastian Klein en smule. Hans formål med programmet var næppe, at det kunne give en indsigt i hvordan kombinatorikken i matematikken opfører sig, men mere at gøre op med den gængse rugbrødsmad og fortælle børnene, at det var okay at eksperimentere og lege med maden, hvilket fik mange forældre til at klage til Danmarks Radio. Hans tilgang til skiftet mellem det normale og det eksperimentelle viser sig dog at give en god måde til at forstå begreber i kombinatorikkens verden. De eksempler, der er belyst i denne artikel, har det tilfælles at de tager udgangspunkt i, at man kan udvælge objekter fra n mulige forskellige objekter. Det er ikke alle tilfælde hvor det kan garanteres, at der ikke er nogle objekter, som er ens. Det munder ud i, at de formler, som man har benyttet sig af i denne artikel, ikke er tilstrækkelige, når der er flere forskellige objekter at vælge imellem. Ligeså er formlerne heller ikke nok til at beskrive sandsynligheder ud fra kombinatorikken, som også er et stort emne inden for denne gren af matematikken. Grunden til dette er, at man først skal kende antallet at udfald, før man kan finde en sandsynlighed for et bestemt udfald. Så selvom et spørgsmål om hvor mange måder et sæt af objekter kan sættes sammen kan lyde elementært, ligger der meget videnskab i det.

Start debatten med en kommentar