I forrige udgave af MatOnline satte artiklen ”Vækst: Når tallene vokser” fokus på eksponentiel vækst. Et simpelt og urealistisk eksempel på eksponentiel vækst er, at vi sætter 1 kr. i banken til en årlig rente på 100 %, som tilskrives ved udgangen af året. Så vil vi efter et år have 20 kr. Men hvad nu hvis banken i stedet for at tilskrive rente ved udgangen af året gjorde det mere regelmæssigt? Lad os forestille os at banken beslutter at tilskrive renter to gange om året til en rente på 50 %. Så vil vi efter et halvt år have 1,50 kr. Og efter et år 2,25 kr. ikke dårligt! Endnu bedre bliver det med en månedlig rente på en tolvtedel. Her vil vi have 2,71 kr. efter år. Vi kunne så fortsætte med en ugentlig rente, en daglig rente etc. og forbedre vores indestående omend forøgelsen bliver mindre i hvert trin. Det viser sig at det bedste resultat, vi kan opnå, er omkring 2,71828 kr. Dette tal er faktisk et såkaldt irrational tal ligesom tallet π, altså et tal der ikke kan skrives som et endeligt decimaltal med systematiske decimaler. Det fortsætter simpelthen i uendelighed efter decimalkommaet. Tallet kaldes Eulers tal efter den berømte schweiziske matematematiker Leonhard Euler (1707-1783) og betegnes med e. Tallet optræder ikke kun i forbindelse med rentesregning. Eulers tal optræder i talrige matematisk udtryk, herunder i formlen for den klokkeformede graf, der omtales i artiklen om verden på grafer i denne udgave af MatOnline. Det for ikke matematikere komplicerede formel ser således ud:
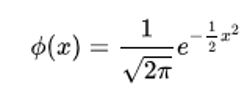
Eulers tal har også mange prakiske anvendelser. Således har det en central betydning i den matematiske teknik kaldet Fourier analyse, der bl.a. anvendes af forskere til at undersøge krystaller ved at bestråle dem med Röntgenstråler. Anvendelse af analysen på de af bestrålingen fremkomne mønstre kan afdække strukturer i molekyler, som fx DNA. Eulers tal indgår også i en række fysiske formler og i formler, der beskriver vækst.
Leonhard Euler satte matematikken på formler og typisk i form af ligninger. Før 1700-tallet eksisterede der stort set ingen formler i naturvidenskaben. Men gradvist blev naturvidenskaben matematiseret. Symboler for fysiske og matematiske størrelser blev forbundet ned bl.a. gange- og lighedstegn i kompakte og sammenhængende formler og skabte derved et nyt tegnsprog i matematikken og naturvidenskaben. Det var et gennembrud for naturvidenskaben. Leonhard Euler var en af foregangsmændene i udviklingen af matematikkens formelsprog. Han var 1700-tallets vigtigste matematiker og til dato den mest produktive med op mod 30.000 sider i alt om matematik. Han beskæftigede sig også med emner som astronomi og mekanik og løste mange konkrete konstruktionsopgaver, bl.a. for den russiske zar.
Da Eulers tal er et irrationalt tal med et uendeligt antal decimaler, kan det ikke uden videre beregnes, men der er talrige metoder til at bestemme en tilnærmet værdi. Fx er det muligt med et en lommeregner, et regneark e.lign. at bestemme en tilnærmet værdi for e ved denne metode: Vi tager udgangspunkt i formlen (1 + 1/n)n .
Først sætter vi n = 1 og får (1 + 1/1)1 = 2.
Så sætter vi n = 2 og får (1 + 1/2)2 = 2,25.
Så tager vi n = 3, n = 4, og sådan fortsætter vi. Jo større n bliver desto tættere, kommer vi på e.
Og den opmærksomme læser har nok noteret, at metoden svarer til indledende eksempel om rentetilskrivning.


Start debatten med en kommentar