In der ersten Ausgabe von MatOnline haben wir im Artikel „Wachstum: Wenn Zahlen anwachsen“ das exponentielle Wachstum betrachtet. Ein einfaches und unrealistisches Beispiel für ein exponentielles Wachstum ist dieses: Wir könnten eine Krone zur Bank bringen und mit einem jährlichen Zinssatz von 100 % anlegen, der uns am Jahresende gutgeschrieben wird. Nach einem Jahr hätten wir so 20 Kronen auf der Bank. Was wäre aber, wenn die Bank die Zinsen nicht am Jahresende gutschreiben würde, sondern öfter? Stellen wir uns einmal vor, die Bank würde beschließen, zweimal im Jahr einen Zinssatz von 50 % gutzuschreiben. Dann hätten wir nach einem halben Jahr 1,50 Kronen auf der Bank. Nach einem Jahr wären es schon 2,25 Kronen. Nicht schlecht! Noch besser wäre ein monatlicher Zins von einem Zwölftel. Hier hätten wir nach einem Jahr 2,71 Kronen. Das könnten wir mit wöchentlichen Zinsen, täglichen Zinsen, etc. weiter fortführen und unser Guthaben immer mehr steigern, auch wenn unser Zugewinn auf jeder Stufe kleiner wird. Letztendlich wird sich zeigen, dass das beste erreichbare Ergebnis bei ca. 2,71828 Kronen liegt. Diese Zahl ist faktisch eine so genannte irrationale Zahl, wie auch die Zahl π – eine Zahl also, die nicht als endliche Dezimalzahl mit systematischen Dezimalstellen aufgeschrieben werden kann. Sie geht hinter dem Komma einfach unendlich weiter. Bekannt ist unsere hier betrachtete Zahl unter dem Namen „Eulersche Zahl“, benannt nach dem berühmten Schweizer Mathematiker Leonhard Euler (1707-1783). Angegeben wird sie mit einem „e“. Und sie tritt nicht nur in Verbindung mit der Zinsberechnung auf. Die Eulersche Zahl findet sich in vielen Termen, wie etwa in der Formel für Glockenkurven, die in dieser Ausgabe von MatOnline im Artikel „Die Welt in Graphen“ behandelt wird. Ihre für Nicht-Mathematiker kompliziert wirkende Formel sieht folgendermaßen aus:
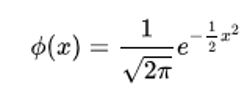
Die Eulersche Zahl lässt sich auch in der Praxis in vielen Bereichen anwenden. Von zentraler Bedeutung ist sie beispielsweise in der als „Fourier-Analyse“ bekannten mathematischen Technik, die von Forschern unter anderem dazu verwendet wird, Kristalle zu untersuchen, indem man sie Röntgenstrahlen aussetzt. Durch die Analyse der durch die Bestrahlung entstehenden Muster kann man Strukturen in Molekülen enthüllen, wie beispielsweise DNA. Auch in einer Reihe von physikalischen und ein Wachstum beschreiben Formeln ist die Eulersche Zahl zu finden.
Leonhard Euler ersann für die Mathematik Formeln, die üblicherweise in Form von Gleichungen gehalten waren. Vor dem 18. Jahrhundert hatte es in der Naturwissenschaft im Großen und Ganzen keine Formeln gegeben. Doch dann wurde die Naturwissenschaft Stück für Stück mathematisiert. Symbole für physikalische und mathematische Größen wurden unter anderem mit Mal- und Gleichheitszeichen zu kompakten und zusammenhängenden Formeln kombiniert, wodurch in der Mathematik und in der Naturwissenschaft eine neue Zeichensprache entstand. Es war ein Durchbruch für die Naturwissenschaft. Und Leonhard Euler gilt als einer der Vorreiter in der Entwicklung der Formelsprache der Mathematik. Er war der bedeutendste Mathematiker des 18. Jahrhunderts und mit insgesamt 30.000 Seiten zum Thema Mathematik auch bis heute der produktivste. Darüber hinaus beschäftigte er sich außerdem mit Themenbereichen wie der Astronomie und der Mechanik und löste viele konkrete Konstruktionsprobleme, unter anderem für den russischen Zaren.
Da die Eulersche Zahl eine irrationale Zahl mit einer unendlichen Anzahl an Dezimalstellen ist, kann sie nicht ohne Weiteres berechnet werden. Aber es gibt zahlreiche Methoden, um einen Näherungswert zu bestimmen. So ist es beispielsweise mit einem Taschenrechner, einem Kalkulationsprogramm oder etwas Ähnlichem möglich, mit der folgenden Methode einen Näherungswert für e zu errechnen: Unser Ausgangspunkt ist die Formel (1 + 1/n)n . Zuerst definieren wir n als 1 und erhalten: (1 + 1/1)1 = 2. Dann definieren wir n als 2 und erhalten: (1 + 1/2)2 = 2,25. Es folgen n = 3, n = 4 und so weiter. Je größer n wird, desto mehr nähern wir uns e an. Und der aufmerksame Leser wird schon bemerkt haben, dass diese Methode dem einleitenden Beispiel zur Berechnung der Zinsen entspricht.


Gib den ersten Kommentar ab