In diesen Zeiten sind die Medien voll mit mathematischen Modellen. Und die mathematischen Modelle bilden die Grundlage für die Beschlüsse, die die Behörden und Politiker in Bezug auf die Entwicklung der COVID-19-Pandemie treffen. Aber wie machen sie das eigentlich? Dieser Artikel wird dir eventuell dabei helfen, das etwas besser zu verstehen. Aber du wirst die Beispiele und Modelle aus diesem Artikel NICHT nutzen können, um eine präzise Prognose zur Entwicklung der COVID-19-Pandemie zu erstellen, da sich die Beispiele nur zu einem gewissen Grad auf die Wirklichkeit beziehen. Außerdem sind die im Artikel angeführten Modelle deutlich einfacher gehalten als die, mit denen die Behörden arbeiten. Im Gegenzug kannst du aber etwas darüber erfahren, wie die Behörden ganz grundsätzlich mathematische Modelle verwenden, um vorherzusagen, wie sich die Anzahl der Infektionsfälle bei einer Pandemie wie dieser entwickelt.
Was versteht man unter mathematischer Modellierung?
Ein mathematisches Modell ist eine mathematische Beschreibung von Zusammenhängen, die aus Formeln, Gleichungen, Termen und entsprechenden Elementen besteht und die man einsetzen kann, um zu einem real existierenden Problem Berechnungen anzustellen und Prognosen zu entwerfen. Die mathematische Modellierung ist, hiervon abgeleitet, die Arbeit an der Erstellung und Anwendung eines mathematischen Modells. Diese Arbeit kann man etwas vereinfacht in drei Teilschritte aufgliedern, die in der folgenden Abbildung durch Pfeile dargestellt werden.
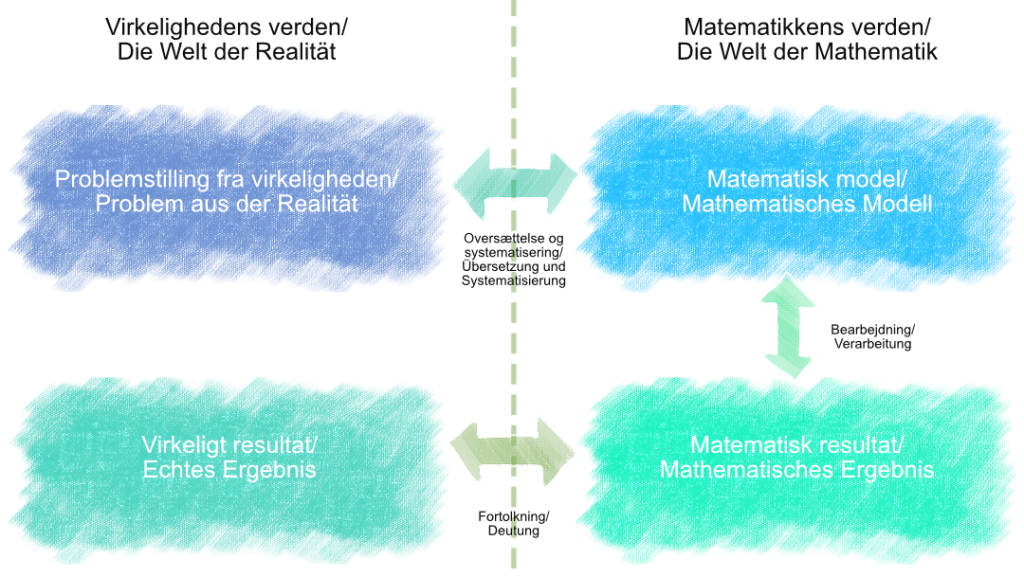
Der dunkelblaue Pfeil ist der erste Teilschritt. Hierbei geht es darum, ein Problem oder eine in der Wirklichkeit auftretende Situation zu systematisieren und in ein mathematisches Modell zu übertragen. Im Hinblick auf die für diesen Artikel gewählte Problemstellung soll unser Ausgangspunkt der sein, zu untersuchen, welche Parameter für die zu erwartende Ausbreitung des Coronavirus von Bedeutung sein könnten. Die Realität zeigt sich oftmals sehr komplex, wenn man Berechnungen zu ihr anstellen möchte, weshalb man in diesem Schritt viele Punkte ein- oder ausschließen muss, um die ansonsten so komplexe Wirklichkeit zu vereinfachen. Letztendlich erhält man bei diesem Schritt ein System aus Parametern, die in die Mathematik übertragen und zu einem mathematischen Modell zusammengestellt werden müssen, das dann im nächsten Schritt zum Einsatz kommen kann.
In diesem Schritt – dem türkisfarbenen Pfeil – kann das erstellte mathematische Modell verwendet werden, um mathematische Berechnungen der Wirklichkeit vorzunehmen, deren Ausgangspunkt eine konkrete Zahl ist. Dafür bedarf es der mathematischen Bearbeitung.
Im dritten und letzten Schritt des Prozesses – dem grünen Pfeil – muss die mathematische Berechnung gedeutet werden, um wieder ein auf die Wirklichkeit bezogenes Ergebnis zu erhalten. Anschließend kann es notwendig werden, den Prozess noch einmal zu überprüfen und die Systematisierung und/oder das mathematische Modell zu verändern, damit das Ergebnis genauer ausfällt.
Bei der COVID-19-Pandemie wird das mathematische Modell in ständig wiederholten Modellierungsverfahren laufend korrigiert. Wir erfahren immer mehr darüber, wie sich die betrachteten Variablen aufeinander auswirken – wie ansteckend das Virus ist, wie sich die Bevölkerung verhält, wie wirkungsvoll die verschiedenen Maßnahmen sind, usw. Je besser wir das Problem verstehen, desto besser können wir es mathematisch beschreiben. Genau das gleiche gilt auch für den meteorologischen Wetterbericht: Je genauer die Wetterdaten sind und je besser unser Verständnis der Wetterphänomene ist, desto genauer wird auch der Wetterbericht.
Weshalb ist die Basisreproduktionszahl so wichtig?
Eines der vielen Modelle, das besonders im März, zu Beginn der Pandemie, in den deutschen und dänischen Medien immer wieder aufgetaucht ist, war die „steile“ und die „flache“ Kurve. Die Kurven haben mögliche Szenarien in der Entwicklung der Infektionen beschrieben. Wie die Kurve letztlich tatsächlich aussieht, hängt unter anderem von der Basisreproduktionszahl ab.
Die Basisreproduktionszahl verrät uns, wie viele Menschen ein Infizierter im Zuge seiner Infektion wiederum selbst infiziert. Eine Basisreproduktionszahl von 2 bedeutet dabei, dass ein Infizierter in der Zeit zwischen eigener Ansteckung und völliger Gesundung im Durchschnitt 2 weitere Personen ansteckt. Die 2 neu infizierten Menschen erkranken ebenfalls und stecken wiederum jeweils 2 andere Personen an. Das ergibt im dritten Glied insgesamt 2 x 2 = 4 Neuinfizierte, die krank werden und die Infektion im Rahmen einer Infektionskette weitergeben. Die Anzahl der Infizierten wird in diesem Fall innerhalb relativ weniger Glieder dramatisch ansteigen. In der Mathematik bezeichnet man einen solchen Vorgang als „exponentielles Wachstum“.
Unter der Voraussetzung, dass die Basisreproduktionszahl bei 2 liegt und ein Infizierter fünf Tage Zeit hat, um weitere Menschen anzustecken, werden wir uns nun einmal näher ansehen, wie viele Infektionen ein infiziertes Liebespaar in 30 Tagen auslösen kann.
Das Liebespaar wurde von einem Unbekannten infiziert und hat keine unmittelbaren Symptome. Deshalb gehen sie ganz unbekümmert ins Kino. Auf dem Weg ins Kino infiziert einer der beiden zunächst einmal einen Fahrgast, der mit ihnen zusammen im Bus unterwegs ist. Dann infizieren sie die Frau, die im Kino die Eintrittskarten kontrolliert, und eine weitere Person, die im Kino neben ihnen sitzt. Auf dem Weg zum Bus, mit dem sie wieder nach Hause fahren möchten, begegnet ihnen schließlich noch ein Freund, den sie ebenfalls anstecken. Zu Hause gehen sie ins Bett, wachen mit Fieber auf und bleiben zu Hause, bis sie wieder gesund sind. Nach diesem Kinobesuch sind also 4 weitere Menschen infiziert. Das entspricht einer Basisreproduktionszahl von 2, da ein Infizierter im Durchschnitt 2 Neuinfektionen ausgelöst hat und 2 Infizierte demnach 4 Menschen angesteckt haben. Die 4 Neuinfizierten, die sich aus dem Kinobesuch des Liebespaares ergeben haben, werden krank und geben die Infektion in der Kette weiter. Da sich die Anzahl der Neuinfektionen in jedem Glied verdoppelt, sehen die Zahlen nach 30 Tagen folgendermaßen aus:

Eine Basisreproduktionszahl von 2 wird insgesamt dazu geführt haben, dass in einer Kette, die mit nur 2 Infizierten begonnen hat, nach 30 Tagen im 7. Glied 128 Menschen neu angesteckt wurden. Diese 128 Menschen können die Infektion in einer exponentiell wachsenden Infektionskette weitertragen, wenn die Basisreproduktionszahl nicht gesenkt wird.
Die Behörden versuchen, die Basisreproduktionszahl zu minimieren. Dadurch sollen ältere und besonders gefährdete Menschen geschützt werden. Außerdem möchte man auf diese Weise dafür sorgen, dass in den Krankenhäusern genügend Kapazitäten frei bleiben, um denjenigen helfen zu können, die Hilfe brauchen. Das hat dazu geführt, dass das gesellschaftliche Leben in vielen Ländern ganz oder teilweise heruntergefahren worden ist und ganz allgemein die Empfehlung ausgesprochen wurde, körperlich Abstand voneinander zu halten und die Hygiene in vielerlei Hinsicht zu verstärken. Mit einem solchen Herunterfahren wurde das Kontaktniveau verringert. Das bedeutet, dass ein Infizierter weniger neue Infektionen auslösen kann, da er ganz einfach mit weniger Menschen in Kontakt steht. Die Basisreproduktionszahl ist unter anderem auch vom Kontaktniveau der Bevölkerung abhängig. Die auf verschiedenen Ansätzen beruhenden Berechnungen zum erwarteten Kontaktniveau und der Basisreproduktionszahl sind ein wichtiger Bestandteil der Systematisierung der Behörden bei der Erstellung eines Modells, mit dem man die Entwicklung der Infektionszahlen berechnen kann.
Wenn wir uns vorstellen, dass ein infizierter Mensch nun nicht mehr durchschnittlich 2 Personen anstecken kann, sondern aufgrund verschiedener Maßnahmen nur noch 1,5, dann erscheint dieser Rückgang um durchschnittlich 0,5 Personen pro Infiziertem erst einmal ziemlich geringfügig. Aber in einer exponentiellen Kurve wirkt er sich sehr schnell massiv auf die Anzahl der Infizierten aus.
In unserem Beispiel mit dem Liebespaar nehmen die beiden nun das eigene Auto und nicht mehr den Bus, um zum Kino zu kommen. So verringert sich ihr Kontaktniveau und dadurch auch die Basisreproduktionszahl. Da sie nicht mehr den Bus nehmen, bleibt der unbeteiligte Fahrgast ohne Infektion. Allerdings infizieren sie immer noch die Frau, die die Eintrittskarten kontrolliert, und den anderen Kinobesucher. Auch den Freund treffen sie nach wie vor, obwohl sie mit dem Auto nach Hause fahren, und stecken ihn an. Deshalb haben wir nun statt 4 nur noch 3 Neuinfizierte. Aber welche Auswirkungen hat das auf lange Sicht? Bei einer Basisreproduktionszahl von 1,5 sieht die Entwicklung innerhalb von 30 Tagen folgendermaßen aus:

Selbstverständlich kann es im dritten Glied in der Wirklichkeit keine 4,5 Neuinfizierten geben, da ein Mensch nicht nur zur Hälfte infiziert sein kann. Aber da mit Durchschnittswerten gerechnet wird, ergibt sich aus dieser mathematischen Berechnung eine Dezimalzahl, wenn man hier bei jedem Glied mit 1,5 multipliziert. Bei einer Basisreproduktionszahl von 1,5 haben wir nach 30 Tagen 22,8 Neuinfizierte, was wir bei einer Rückübertragung in die Wirklichkeit als ca. 23 Neuinfizierte im siebten Glied deuten würden. Das sind 105 Personen weniger als bei einer Basisreproduktionszahl von 2, wo wir im siebten Glied 128 Neuinfektionen hatten. So konnten wir die Belastung der Krankenhäuser deutlich verringern, indem wir ganz einfach nur die Basisreproduktionszahl ein ganz kleines bisschen nach unten gedrückt haben. Die folgende Grafik mit den 2 Kurven zeigt die Entwicklung der Neuinfektionen nach jeweils 5 Tagen im Vergleich.
Wenn die Basisreproduktionszahl unter 1 fällt, werden immer weniger Menschen angesteckt und die Anzahl der Kranken geht Stück für Stück zurück. Das ist möglich, wenn wir uns an die Vorgaben zur sozialen Distanz und zu einer besseren Hygiene halten und wenn wir eine Herdenimmunität entwickeln.
Eine Basisreproduktionszahl von 2 hat im Vergleich zu einer Basisreproduktionszahl von 1,5 nach 30 Tagen einen Unterschied von ca. 105 Neuinfektionen ergeben, und das ausgehend von nur 2 Infizierten an Tag 0. Hätten wir nun einen Zeitraum von 60 Tagen mit einer Basisreproduktionszahl von 2 bzw 1,5, wäre der Unterschied erheblich größer gewesen. Nach 60 Tagen hätten die 2 Infizierten bei einer Basisreproduktionszahl von 2 im 13. Glied (Tag 60) 8.192 Neuinfektionen ausgelöst, bei einer Basisreproduktionszahl von 1,5 wären es nur 259 Neuinfektionen gewesen. So haben wir also 60 Tage nach dem Kinobesuch unseres Liebespaares den ganz massiven Unterschied von 7.933 Infizierten. Allein aufgrund der Differenz im exponentiellen Wachstum der Infektionszunahme. Hätte die Basisreproduktionszahl ein wenig höher gelegen – beispielsweise bei 2,5 – dann hätten wir nach 60 Tagen im 13. Glied ganze 119.209 Neuinfektionen. Deshalb sind die Behörden und Politiker sehr darum bemüht, mehr über die Basisreproduktionszahl zu erfahren und sie zu senken, damit das Gesundheitssystem nicht überlastet wird.
Die „steile“ und die „flache“ Kurve
Man nimmt an, dass man die Krankheit auf zwei verschiedene Arten aufhalten kann. Beide machen es erforderlich, dass die Basisreproduktionszahl Schritt für Schritt fällt, bis sie 0 erreicht. Eine Möglichkeit, die Basisreproduktionszahl zu senken und damit die Krankheit zu stoppen, sind Maßnahmen wie Abstand, bessere Hygiene, Infektionsnachverfolgung und Quarantäne. Das erfordert jedoch ein durchgreifendes und systematisches Vorgehen, das über einen langen Zeitraum aufrecht erhalten werden muss. Die zweite Möglichkeit ist die Herdenimmunität. Das bedeutet, dass ein ausreichend großer Teil der Bevölkerung infiziert gewesen ist und eine Immunität entwickelt hat, wodurch es für die Krankheit schwieriger wird, sich zu verbreiten. Denn wer immun ist, kann sie nicht mehr weitergeben. So treffen diejenigen, die noch nicht infiziert waren, kaum noch auf Menschen, bei denen sie sich anstecken könnten. Dadurch sinkt die Basisreproduktionszahl, und mit der Zeit hört die Krankheit auf, sich weiter zu verbreiten. Eine solche Herdenimmunität kann auch durch Impfungen erreicht werden, aber für COVID-19 ist bisher keine Impfung entwickelt worden.
Wir gehen davon aus, dass 60 % (in Dänemark ist man bei der Corona-Pandemie frühzeitig von 60-70 % ausgegangen) einer Bevölkerungsgruppe infiziert oder gegen eine bestimmte Krankheit geimpft worden sein müssen, damit eine Herdenimmunität erreicht wird. In einem Land mit 1.000.000 Einwohnern müssen also 600.000 Einwohner (60 %) die Krankheit gehabt haben, wenn keine Impfung zur Verfügung steht. Erst dann gibt es eine Herdenimmunität. Wenn jetzt aber diese 600.000 Personen in einem sehr kurzen Zeitraum angesteckt werden, wird das die Krankenhäuser des Landes überfordern. Dieses Szenario ist die „steile Kurve“, die bei einer hohen Basisreproduktionszahl entsteht. Wenn wir die Basisreproduktionszahl senken, müssen immer noch 600.000 Menschen die Krankheit gehabt haben, damit wir eine Herdenimmunität erreichen, aber sie erkranken über einen wesentlich längeren Zeitraum hinweg und belasten das Gesundheitssystem nicht so stark, da nicht so viele Kranke gleichzeitig auftreten. Das ist die „flache Kurve“. Es bestehen jedoch Zweifel daran, ob es möglich sein wird, bei der COVID-19-Pandemie eine Herdenimmunität zu erreichen.
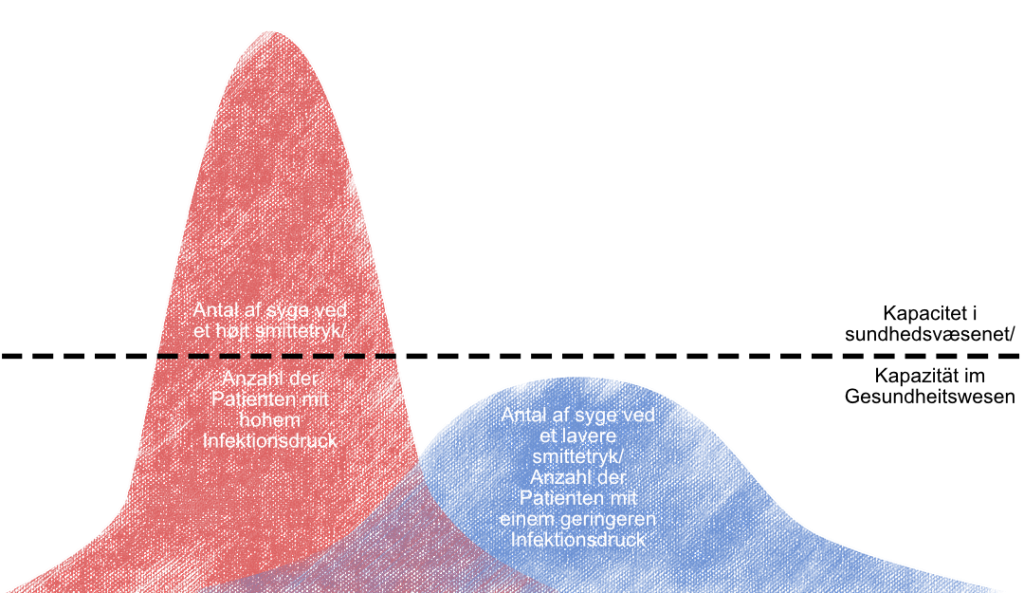
Wenn wir in Erfahrung bringen möchten, ob das Gesundheitssystem eines Landes mit der Anzahl der Kranken zurechtkommen kann, müssen wir uns in der Realität erheblich mehr Parameter ansehen als nur das Kontaktniveau und die Basisreproduktionszahl. Darüber hinaus sind das Kontaktniveau und die Basisreproduktionszahl bei den verschiedenen Bevölkerungsgruppen auch nicht unbedingt gleich. Ein kleines Krippenkind hat vermutlich ein erheblich geringeres Kontaktniveau als beispielsweise seine Eltern. Junge Menschen haben vermutlich ein höheres Kontaktniveau als ältere. Manche Altersgruppen sind eventuell generell ansteckender als andere, usw. Es gibt schlichtweg unzählige Parameter, die wir beachten müssen, wenn wir ein brauchbares mathematisches Modell erstellen wollen, das uns etwas über die Entwicklung der Infektionszahlen verraten kann. Dazu gehören beispielsweise die Inkubationszeit, die Länge des Krankheitsverlaufs, die Länge des Zeitraums, in dem ein Infizierter andere Menschen anstecken kann, und vieles mehr.
Wenn die Länder sich nach und nach wieder mehr öffnen, werden Experten damit beschäftigt sein, mathematische Modelle anzuwenden, um mögliche Veränderungen des Kontaktniveaus und der Basisreproduktionszahl zu berechnen. Die Berechnungen werden auf qualifizierten Schätzungen fußen, aber sie werden auch voller Unsicherheiten stecken. Denn ein mathematisches Modell kann niemals genauer sein als die Daten und das Wissen, die ihm zugrunde liegen. Ob die Prognosen richtig waren, werden wir also erst wissen, wenn wir die Pandemie hinter uns gebracht haben.
Passt gut auf euch selbst und auf die anderen auf – mit Abstand.
Mehr über die Modelle, die hinter den Berechnungen der dänischen Behörden stecken, kannst du hier erfahren:
„Modellberechnungen für Szenarien bei einer Wiedereröffnung von Dänemark“
Dort kannst du dir ansehen, wie sich die Szenarien und Prognosen von Anfang April bis Ende Mai verändert haben – genau so, wie sich auch der Wetterbericht von Tag zu Tag ändert, wenn die Meteorologen Erkenntnisse dazu gewinnen.

Gib den ersten Kommentar ab