Im ersten Artikel mit mathematischen Linienrätseln haben wir uns Aufgaben angesehen, bei denen es darum ging, Figuren jeweils nur mit einem langen Strich zu zeichnen. Vielleicht bist du darauf gekommen, dass nur zwei dieser Figuren mit einem Strich gezeichnet werden konnten, ohne den Bleistift zwischendurch abzusetzen.
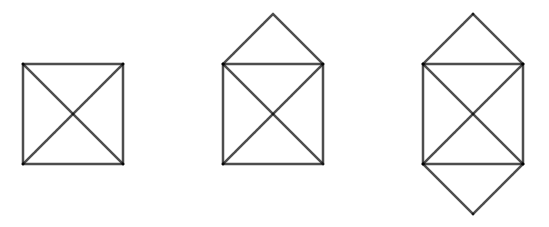
Der Trick, den wir angewendet haben, um die Aufgaben zu lösen – die Valenz der Knotenpunkte zu zählen (also die Anzahl der Seiten, die mit einem Punkt verbunden sind) – gehört zu einem Teilgebiet der Mathematik, das als Graphentheorie bezeichnet wird. Hier soll der Begriff Graph die oben dargestellten Figuren bezeichnen.
Achtung: Graphen kennen die meisten als Kurve in einem Koordinatensystem. In der letzten Zeit haben wir diese Art von Graphen immer wieder in den Nachrichten gesehen, wenn darüber berichtet wurde, wie stark sich Covid-19 ausbreitet. Aber um diese Graphen geht es in diesem Artikel nicht. In diesem Artikel besteht ein Graph aus Punkten und Seiten, wobei eine Seite zwei der Punkte des Graphen verbindet.
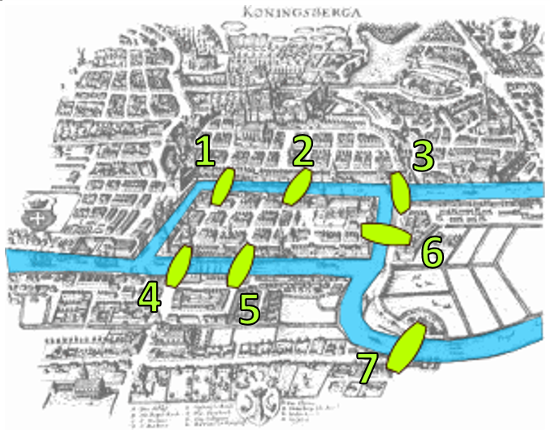
Es war der bekannte Mathematiker Leonhard Euler, der 1736 den Startschuss für die Begründung der Graphentheorie gab, als er sich dem klassischen Problem der sieben Brücken in der Stadt Königsberg widmete und dafür eine Lösung fand. Königsberg heißt heute Kaliningrad und ist eine russische Stadt, die nördlich von Polen liegt – dort, wo der Fluss Pregolja in die Ostsee mündet.
Zu Eulers Zeiten war es Tradition, abends über die Brücken der Stadt zu bummeln. Wie man auf dem Bild erkennen kann, haben diese sieben Brücken die verschiedenen Stadtteile miteinander verbunden. Die Nummerierung der Brücken soll hier nur dazu dienen, dass man sie voneinander unterscheiden kann.
Die Frage, die Euler sich stellte, war folgende:
- Ist es möglich, einen Spaziergang zu machen und dabei alle sieben Brücken genau einmal zu überqueren?
Versuche einmal selbst, einen solchen Weg ausfindig zu machen.
Wie hat Euler das Problem gelöst?
Er hätte beispielsweise all die Möglichkeiten, die Brücken in unterschiedlicher Reihenfolge zu überqueren, mühselig eine nach der anderen ausprobieren können. Ein Teil der Varianten wäre physisch unmöglich gewesen, da etwa Brücke 1 und Brücke 7 nicht direkt aufeinander folgen können, denn sie verbinden ja unterschiedliche Stadtteile. Außerdem muss man nur die Hälfte der Möglichkeiten durchprobieren, denn wenn man einen Weg in die eine Richtung nicht nehmen kann, kann man ihn auch in die andere Richtung nicht nehmen. Wenn beispielsweise die Streckenführung 1-2-3-4-5-6-7 nicht möglich ist, kann 7-6-5-4-3-2-1 auch nicht funktionieren.
Euler löste das Problem nicht, indem er alle Möglichkeiten durchging, sondern indem er überlegte. Das Kluge an seinem Gedankengang war, dass er nicht darüber nachdachte, wo die Brücken lagen, sondern nur darüber, welche Stadtteile sie miteinander verbanden.
Jeden Stadtteil betrachtete er als Knotenpunkt und jede Brücke als eine Seite zwischen den zwei jeweiligen Knotenpunkten. Auf diese Weise machte er aus einer komplizierten Karte der Stadt einen einfachen Graphen zu ihren Brücken:
Aber auch bei nur sieben Brücken wäre es eine langwierige Aufgabe gewesen, alle Möglichkeiten von vorne bis hinten durchzuspielen, denn es gibt verschiedene Anordnungen. Eine solche Anordnung nennt man in der Mathematik eine „Permutation“:
https://www.dcode.fr/permutations-generator
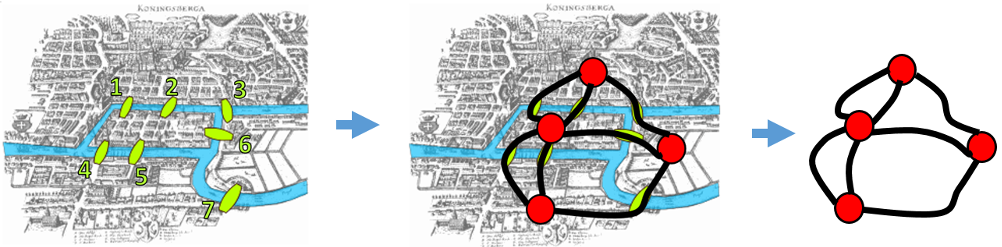
Jetzt war die Aufgabe auf etwas reduziert, das wir lösen können, indem wir uns die Valenz der Knotenpunkte ansehen, was wir bereits im ersten Artikel zu mathematischen Rätseln getan haben. Euler war, soweit wir wissen, der erste, der diesen Gedankengang benutzte. Und er fand heraus, was auch du sicherlich mittlerweile herausgefunden hast – dass es nicht möglich war, einen abendlichen Spaziergang zu machen, bei dem man alle Brücken genau einmal überquerte.
Wie ist es heute?
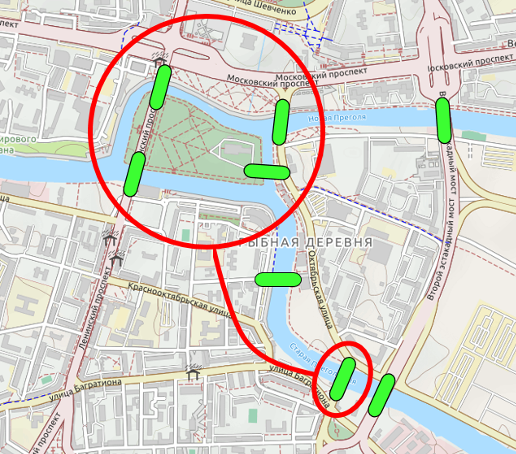
Wenn wir uns eine aktuelle Karte von Kaliningrad ansehen, erkennen wir, dass sich die Lage geändert hat. Einige Brücken sind verschwunden, andere sind hinzugekommen. Die Brücken, die rot eingekreist sind, entsprechen alten Brücken, die immer noch existieren. Brücke 2 und Brücke 5 der alten Karte gibt es nicht mehr.
Wenn Euler heutzutage in Kaliningrad wohnen würde, könnte er dann wohl seinen Wunschspaziergang über die 5 verbliebenen Brücken machen (jene Brücken, die rot eingekreist sind)?
Wie sieht es aus, wenn wir die drei neuen Brücken mit einbeziehen, sodass es insgesamt acht Brücken sind? Kann er dann von zu Hause aus losgehen und auch wieder dort ankommen – und macht es einen Unterschied, wo er wohnt?
Die letzte Aufgabe aus dem ersten Artikel
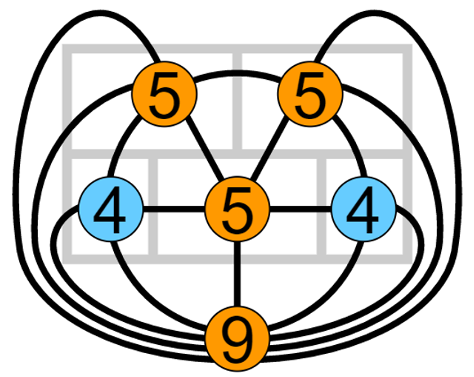
Es ging darum, alle 16 Wände mit einem Strich genau einmal zu durchkreuzen. Wenn du dich bislang noch nicht mit der Aufgabe beschäftigt hast, dann ist jetzt ein guter Zeitpunkt. Hier siehst du einen Versuch, der auf jeden Fall keine Lösung ist.
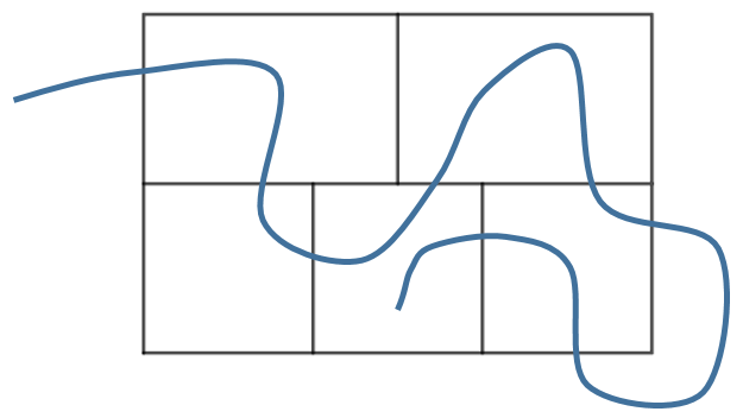
Wir haben 16 Wände. Insgesamt ergibt das:
16!=16·15·14·13·12·11·10·9·8·7·6·5·4·3·2·1=20.922.789.888.000 verschiedene Wand-Reihenfolgen (Permutationen). Wieder reicht es, wenn wir die Hälfte der Möglichkeiten überprüfen, denn jeder Strich deckt zwei Varianten ab, da man an beiden Enden zu zeichnen beginnen kann. Und wieder ist ein Teil der Permutationen von vornherein unmöglich, da nicht alle Wände direkt miteinander verbunden werden können. Aber trotz allem bleiben immer noch Millionen von Möglichkeiten, die es zu prüfen gilt.
Gut, dass Euler herausgefunden hat, wie man in Graphen denkt!
Allerdings gibt es in der Graphentheorie immer noch viele Probleme, von denen wir nicht wissen, wie wir sie lösen sollen. Wie das Beispiel mit den 16 Wänden deutlich zeigt, brauchen wir gar nicht viele Knotenpunkte und Seiten, um eine Anzahl an Möglichkeiten zu erreichen, die so hoch ist, dass selbst unser schnellster und stärkster Computer aufgeben muss.
Stell dir vor, du bist Geschäftsführer von NETTO und sollst alle NETTO-Filialen in Dänemark besuchen. Das sind so um die 500. Du möchtest natürlich die kürzeste Route nehmen, aber wenn du ganz sicher gehen möchtest und alle Möglichkeiten überprüfst, bevor du losfährst, wirst du dich niemals auf den Weg machen!
Die Anzahl der möglichen Strecken, die dich an den 500 Läden vorbei führen, ist eine Zahl mit mehr als 1000 Ziffern (500!≈1,22·101134,
, vgl. die Zahl weiter unten). Eine Milliarde gilt bei den meisten Menschen schon als wirklich große Zahl, aber sie hat nur 10 Ziffern. Selbst wenn Euler damals, im Jahre 1736, einen modernen Computer zur Verfügung gehabt und ihn benutzt hätte, um die Möglichkeiten zu überprüfen, wäre er bis heute kaum zu einem Ergebnis gekommen.
500!=1220136825991110068701238785423046926253574
342803192842192413588385845373153881997605496447
502203281863013616477148203584163378722078177200
480785205159329285477907571939330603772960859086
270429174547882424912726344305670173270769461062
802310452644218878789465754777149863494367781037
644274033827365397471386477878495438489595537537
990423241061271326984327745715546309977202781014
561081188373709531016356324432987029563896628911
658974769572087926928871281780070265174507768410
719624390394322536422605234945850129918571501248
706961568141625359056693423813008856249246891564
126775654481886506593847951775360894005745238940
335798476363944905313062323749066445048824665075
946735862074637925184200459369692981022263971952
597190945217823331756934581508552332820762820023
402626907898342451712006207714640979456116127629
145951237229913340169552363850942885592018727433
795173014586357570828355780158735432768888680120
399882384702151467605445407663535984174430480128
938313896881639487469658817504506926365338175055
478128640000000000000000000000000000000000000000
000000000000000000000000000000000000000000000000
000000000000000000000000000000000000
Die ersten 720 Permutationen der Zahlen 1, 2, 3, 4, 5, 6, 7 – genau die, die mit der Zahl 1 beginnen. Zusatzaufgabe
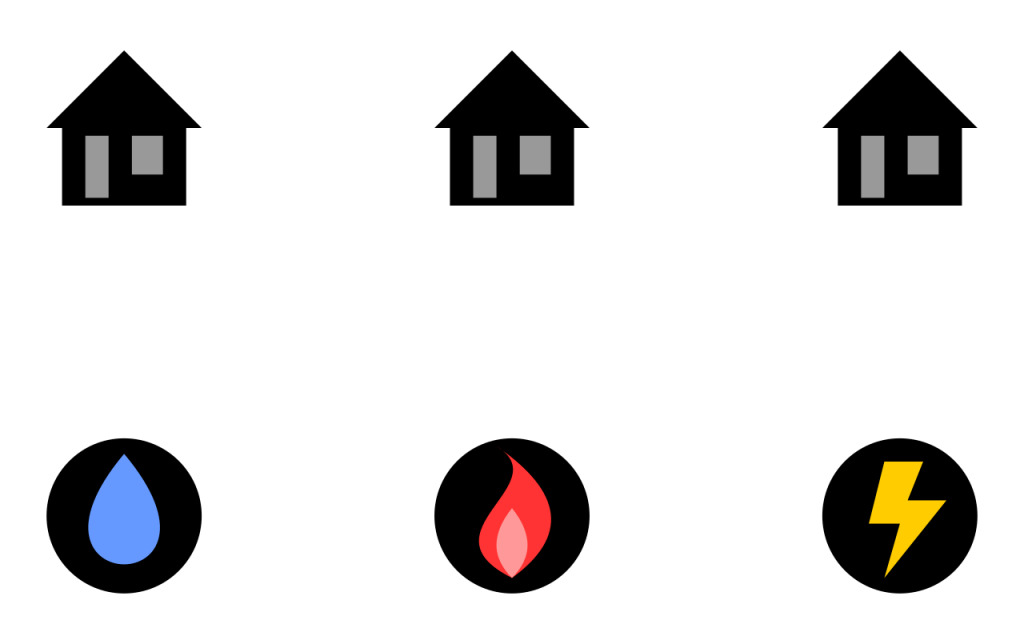
Wir haben drei Häuser, ein Wasserwerk, ein Gaswerk und ein Stromkraftwerk. Diese drei Häuser sollen alle eine direkte Leitung (eingezeichnete Linie) zum Wasserwerk, zum Gaswerk und zum Stromkraftwerk bekommen, damit sie beliefert werden können. Dabei dürfen sich die Leitungen niemals kreuzen.
Bekommst du das hin?


Gib den ersten Kommentar ab