Mathematik und Ethik

Der Begriff ”Ethik” ist zunehmend in aller Munde. In vielen verschiedenen Situationen ist ein Abwägen der ethischen Voraussetzungen und Folgen des eigenen Handelns oder der eigenen Entscheidungen wichtig. Ethik ist für eine Gruppe immer dann von selbstverständlicher Bedeutung, wenn etwa im Parlament eines Landes politische Beschlüsse gefasst oder in der Familie Entscheidungen getroffen werden (müssen). Aber wie passen Ethik und Mathematik ggf. zusammen? Die Mathematik ist relativ rigoros und stringent. Da gibt es nichts zu deuteln. Man mag zwar dafür oder dagegen sein, dass zwei plus zwei gleich vier ist, aber die Mathematik beruht halt auf Gesetzen und Axiomen, die als wahr erwiesen sind und daher nicht Gegenstand einer Widerlegungsdiskussion sein können. Doch wo lässt sich in der mathematischen Forschung nach ethischen Überlegungen suchen, wo hält sich Ethik da ggf. versteckt? Dieser Artikel beleuchtet einige der wichtigsten ethischen Fragen in der Geschichte der Mathematik und möchte veranschaulichen, wie sich diese Frage auf die weitere Erforschung der Mathematik auswirken kann. Mathematik-ethische Fragen lassen sich in zwei Gruppen unterteilen: solche, die sich direkt auf die Forschung beziehen, und solche, die sich indirekt auf die Forschung auswirken können.

Die Ethik des Nützlichen (Utilitarismus):
Entscheidungen müssen auf dem (mutmaßlichen) Ergebnis des Handelns beruhen. Erhöht sich die ‚Menge‘ des Wohlergehens (für alle), so war die Entscheidung ”die richtige”. Die Folgen des Handelns sind daher das Maß für den moralischen Wert dieses Handelns.

Die Ethik der Pflicht, des ‚Gesollten‘ (Deontologie):
Entscheidungen müssen auf Regeln und moralischen Grundsätzen beruhen. ”Das Richtige zu tun” zählt mehr als das Ergebnis, weshalb der moralische Wert des Handelns wichtiger ist als die durch das Handeln herbeigeführten Folgen.

Die ‚Verantwortung‘ der Atombombe

J. Robert Oppenheimer (1894-1967) gilt als Vater der Atombombe, der gegen Ende des Zweiten Weltkriegs zwischen 150.000 und 250.000 Menschen zum Opfer fielen. Er war Physiker und zusammen mit den anderen Mitgliedern des sog. Manhattan-Projekts an der Entwicklung der stärksten Waffe der damaligen Zeit beteiligt. Viele haben später in Frage gestellt, ob Oppenheimer das Richtige getan habe. Er wusste, dass die Waffe zur Kriegsführung eingesetzt werden würde, was letztlich den Tod vieler Menschen, Soldaten wie Zivilisten, zur Folge haben könnte. Aber gleichzeitig ist der Zweck der Wissenschaft das (Weiter)Entwickeln von etwas Bestehendem und das Erzeugen neuen Wissens — das in diesem Fall als Waffe verwendet werden könnte. Diese Diskussion beruht auf den beiden großen Bereichen der Ethik: Utilitarismus und Deontologie.

Verschlüsselung und Sicherheit
Wissenschaft war schon immer auch Waffe, und wer bei der Waffentechnik die Nase vorn hatte, war in aller Regel auch kriegsüberlegen. Insofern stehen Wissenschaftler, deren Erkenntnisse zu Kriegszwecken genutzt werden, immer auch vor der Frage der Ethik.

Wissenschaft war schon immer auch Waffe, und wer bei der Waffentechnik die Nase vorn hatte, war in aller Regel auch kriegsüberlegen. Insofern stehen Wissenschaftler, deren Erkenntnisse zu Kriegszwecken genutzt werden, immer auch vor der Frage der Ethik.

Verschlüsselung ist eine mathematische Anwendung und heute in praktisch allen Bereichen der Elektronik und Sicherheit im Internet gebräuchlich — ein weiteres Beispiel für das Ins-Spiel-bringen der Mathematik in einer ethisch geprägten Diskussion. Und wieder begegnen uns hier Weltgeschichte und Kriegsführung, denn wer in einem Krieg Nachrichten zwischen Verbündeten mit der Gewissheit versenden kann, dass der Feind über die Inhalte im Unklaren verbleibt, ist im Vorteil, und so begannen die Menschen, zu versendende Nachrichten zu verschlüsseln. Verschlüsselung bedeutet die Verwendung von Codes, die es allen Schlüsselunkundigen unmöglich machen, die Nachricht zu lesen. Viele Codes beruhen auf der Multiplikation großer Primzahlen, und zusammen mit den vielen Zahlenkombinationen kann es fast unmöglich sein, den Code zu knacken. Das bekannteste Beispiel für diese Art der Verschlüsselung ist der Enigma-Code.

Enigma war eine 1929 für die Armee entwickelte deutsche Verschlüsselungsmaschine. Im Vorfeld des 2. Weltkriegs wurde die gesamte deutsche militärische Kommunikation damit verschlüsselt.

Wenn es den Briten gelänge, den Code zu knacken, hätten sie Zugang zu allen Nachrichten der Deutschen und damit bessere Chancen, den Krieg zu gewinnen. Das Knacken des Enigma-Codes erfordert jedoch ein hohes mathematisches Können — daher ja die Verwendung dieses Gerätes. Polnische Mathematiker hatten sich bereits in den 1930er-Jahren erfolglos am Code versucht. 1939 richtete Großbritannien gezielt eine Ermittlungseinheit ein, um den Enigma-Code zu entschlüsseln. Die Briten hatten die Vorarbeit der polnischen Mathematiker zur Verfügung bekommen, und die Entschlüsselung gelang. Der Bekannteste aus dieser Einheit war der Mathematiker Alan Turing (1912-1954), der später zur Schaffung der Informatik beitrug — der Lehre von den Daten. 1945 waren die Briten so weit, dass sie fast alle deutschen Nachrichten in wenigen Tagen entschlüsseln konnten.

Dieser Einsatz mathematischer Fähigkeiten half, einen Krieg zu beenden, aber er kann auch Kriege schüren, und heute hat sich die Verschlüsselung als Mittel zur Informationssicherheit entwickelt. Informationen in Form von Daten sind für die meisten Staaten und Privatunternehmen Gold wert, die Sicherheit der Daten für Privatpersonen mithin von größter Bedeutung, da Hacker ggf. auf diese Informationen zugreifen, weshalb die Ethik der Verschlüsselung von wesentlicher Bedeutung ist, da auf diese Weise eigene private Informationen und Sicherheitsinformationen von Staaten geschützt werden.

Wissenschaft und ihre Vermittlung

Für Forschungsarbeiten in jedem Bereich gelten von der Wissenschaft zu beachtende ethische Richtlinien. In Kurzform etwa: keine Plagiate, kein künstliches Aufblähen der Ergebnisse, die Verpflichtung zu hoher fachlicher Qualität. Wegen ihrer Rolle als ”immer richtig” darf die Mathematik nicht falsch eingesetzt werden, da ihre Glaubwürdigkeit (dann) zu falschen Informationen und letztlich hohen wirtschaftlichen Verlusten oder Gewinnen führen kann, was nicht unbedingt im Interesse der Gesellschaft als Ganzes ist. Ein Beispiel dafür gab es 2012 in Dänemark, wo mit der Krankheit Bauchaortenaneurysma gearbeitet wurde, einer Ausstülpung der Hauptarterie in der Bauchhöhle. In schweren Fällen kann die Krankheit zu einer Ruptur (einem Riss) des Aortenaneurysmas mit anschließenden mutmaßlich tödlichen Blutungen in der Bauchhöhle führen. Die Forschung hat gezeigt, dass bei frühzeitiger Diagnose die Ausstülpung chirurgisch entfernt werden kann. Diese vorbeugende OP ist aus gesundheitsökonomischer Sicht billiger als eine Notoperation im Falle einer gerissenen Aorta. Daher erstellte eine Gruppe aus Gesundheitsökonomen ein mathematisches Modell, das die wirtschaftlichen Vor- und Nachteile eines Vorbeugeprogramms für diese Krankheit beschreibt, wobei die Kosten des Programms in drei verschiedene Gruppen unterteilt wurden. Später stellte sich jedoch heraus, dass eine Aufteilung in nur drei verschiedene Gruppen nicht möglich war, da in Dänemark mit sechs verschiedenen Kostengruppen gearbeitet wird, wenn es um die zwischen Staat und Regionen zu teilenden Gesundheitsausgaben geht. Den Gesundheitsökonomen wurde vorgeworfen, die Kostengruppen absichtlich vereinfacht zu haben, um das Bild des Vorbeugeprogramms zu verändern. Am Ende wurden die betreffenden Gesundheitsökonomen von den Vorwürfen freigesprochen, aber der Fall zeigt, dass es viele ethische Überlegungen gibt, die bei der Erstellung eines mathematischen Modells von großer Bedeutung sein können. Mathematische Modelle spielen in der heutigen Gesellschaft eine Rolle, wenn sie aus der Überzeugung heraus, dass die Mathematik solide und überzeugend ist, nicht unbedingt in Frage gestellt werden.

Die Bedeutung mathematischer Modelle zeigt sich in vielen Pressekonferenzen der — in diesem Fall dänischen — Regierung während der Coronapandemie, wo insbesondere ein bekanntes mathematisches Modell zur Ermittlung, wann die Krankenhäuser an ihre Kapazitätsgrenze stoßen würden, zu einem Maßstab für die Glaubwürdigkeit der Mathematik bei den Bürgern wurde. Daher können zu stark vereinfachte und idealisierte Annahmen und Darstellungen bei der Erstellung mathematischer Modelle große Auswirkungen auf die Gesellschaft haben, sowohl in Bezug auf die Glaubwürdigkeit als auch die wirtschaftlichen Aspekte.

Die ‚Redlichkeit‘ von Modellen

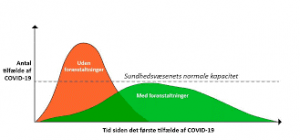
Das „Coronamodell“

Man mag sich fragen, ob die zwangsläufig vorzunehmenden Annahmen und Vereinfachungen bei der Erstellung mathematischer Modelle eine zu große Manipulation ‚der Welt‘ darstellen, aber wenn als Alternative die Probleme — ohne ein vereinfachtes Modell — gar nicht erst geklärt würden, wären wir wieder bei der Frage des ”Nützlichen” und des ”Gesollten”. Und es reift die Erkenntnis, wie wichtig mathematische Modelle sind, wenn es um die Verhütung von Ereignissen geht, die große Auswirkungen auf das eigene Leben oder auf die Wirtschaft einer Gesellschaft haben können. Die COVID-19-Pandemie wie auch die Finanz- und Wirtschaftskrise 2008 sind hierfür gute Beispiele. Mathematische Modelle wurden während der gesamten Pandemie ausgiebig genutzt, um zu beurteilen, wann und in welchem Umfang heruntergefahren werden müsse (Lock-down) und dabei einerseits die Wirtschaft am Laufen zu halten und andererseits sicherzustellen, dass so wenige Menschen wie möglich tödlich erkranken.

Die Finanzkrise 2008 wurde seit ihrem Ende mit verschiedenen mathematischen Modellen eingehend analysiert, um sicherzustellen, dass sich eine ähnliche Krise nicht wiederholen kann. Dieser Sachverhalt verdeutlicht auch die ethische Verantwortung, die mit der Aufstellung eines mathematischen Modells verbunden ist — eben weil der Mathematik diese ihr innewohnende Authentizität vorauseilt.

Dieser Artikel beschreibt Situationen aus dem ”wirklichen Leben”, in denen die mathematische Forschung unter Umständen und in Sachlagen eingesetzt wurde, in denen die Ethik zu einer heillos durcheinandergewirbelten Gemengelage wurde, denn wo ist bzw. sei die Grenze zwischen wissenschaftlicher Entwicklung einerseits und den Folgen, die eine Entdeckung für eine Gesellschaft und das Leben des und der Einzelnen haben kann, andererseits? Auch die ethische Verantwortung der mathematischen Modellierung wurde thematisiert, und auch hier zeigt sich, dass die Entdeckung und Konstruktion neuer Mathematik sowohl aus gesellschaftlicher als auch privater Sicht des und der Einzelnen große Auswirkungen haben kann. Die eingangs gestellte Frage, wie sich dieses Wissen um vergangene Probleme auf die weitere Forschung in der Mathematik auswirken kann, lässt sich nur mit einer Mutmaßung beantworten. Wie immer kann es in mehrere Richtungen gehen, denn die Wissenschaft muss sich mittlerweile mehr ethische/n Fragen stellen, wenn sie sich mit Mathematik beschäftigt. Werden die schlimmsten Beispiele für schreckliche Folgen mathematischer Entdeckungen jemanden veranlassen, seine Entdeckungen (lieber) für sich zu behalten, oder wird die Pflicht, neue Forschung und Kenntniserlangung voranzutreiben, (dann doch) Vorrang haben? Die Zukunft wird es zeigen (müssen). Sicher ist nur, dass man im Universum der Mathematik auch im ethischen ‚Dilemmafahrwasser‘ navigieren können muss — und dass der Ethik eine Rolle in der Mathematikwissenschaft zukommt.

Inspiration: ”Invitation til matematikkens videnskabsteori” von      Mikkel Willum Johansen & Henrik Kragh Sørensen.