Kartentricks mit Mathemagie

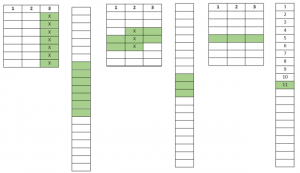
Durch Anordnen der Karten in drei Reihen und Erfragen, in welcher davon die Karte liegt, erfahren Sie, in welchem Teil der Karten sich die ausgewählte Karte befindet; hier in unserem Fall Reihe 3 — die grünen Karten (1).

Im nächsten Teil des Tricks sammeln Sie die drei Reihen zu drei Kartenstapeln. Legen Sie nun Stapel Nr. 3 in die Mitte (2).

Nach erneutem Anordnen der Karten in die drei Reihen liegen die möglichen Karten auf alle drei Reihen verteilt. Sie bitten nun die Person, auf die Reihe mit der gewählten Karte zu zeigen, wo-durch Sie die möglichen Karten auf 2-3 verschiedene Karten eingrenzen. Zeigt die Person auf Reihe 1 oder 3, so ist es eine der beiden grünen Karten, die sich in dem gewählten Stapel befinden. Wird auf Reihe 2 gezeigt, so ist es eine der 3 grünen Karten. Wir haben hier den Fall, dass die gewählte Karte in Reihe 2 liegt, aber natürlich hätte es ebenso gut eine der anderen Reihen sein können (3).

Die Karten werden nun wieder mit dem ausgewählten Stapel in der Mitte angeordnet. In unserem Fall hier informiert uns die Person, dass sich die Karte in Reihe 2 befindet. Es bleiben also drei mögliche Karten übrig, die sich in der Mitte des Stapels (4) befinden.

Wenn Sie die Karten wieder in drei neue Reihen legen, verteilen sich die drei mittleren auf die drei Reihen, so dass sie genau in der Mitte jeder Reihe liegen. Dann bitten wir unsere Person, auf die Reihe mit der gewählten Karte zu zeigen, und damit gibt es nur noch eine mögliche Karte (5).

Wenn wir nun die Karten wieder einsammeln und den Stapel mit der richtigen Karte wieder in die Mitte legen, liegt die Karte nun genau in der Mitte des Stapels als Karte Nr. 11 — unabhängig davon, ob sie in der 1., 2. oder 3. Reihe lag.

Erklärung des Zaubertricks somit: Mathematische Zusammenhänge, Zählen und Logik.

Der zweite Kartentrick

Mit dem Ausführen dieses Kartentricks können Sie mithilfe von ein wenig Mathemagie ‚erraten‘, welche Karte verdeckt liegt. Leider kann man nicht sagen, welche Farbe, sondern nur, welche Zahl die Karte hat bzw. ob es ein Bube (entspricht 11), eine Dame (entspricht 12) oder ein König (entspricht 13) ist.

Was brauchen Sie?

– ein Vollkartenspiel mit 52 Karten; wichtig: alle müssen vorhanden sein, es darf keine fehlen

– eine Person, die Ihnen beim Vorführen assistiert

Was tun Sie?

Zunächst alle Karten auf Stapel verteilen, und zwar folgendermaßen:

1. Irgendeine Karte ablegen, Bildseite nach oben. Ab dem Wert dieser Karte aufwärts bis 13 zählen; mit jeder genannten neuen Zahl eine Karte auf die erste legen, angenommen eine 4, Bildseite nach oben, und dann von da aus weiterzählen: 5, 6, 7, 8, 9, 10, 11, 12 und 13. Somit liegen neun Karten auf der 4 (Bild 5). Nun den Stapel wenden, sodass die Verdecktseite (Rückseite) nach oben zeigt.

2. Weitere Stapel wie unter Pkt. 1 bilden, bis keine Karten mehr übrig sind. Falls doch noch welche da sind (nicht bis 13 hochzählbar), diese überschüssigen auf einen Stapel für sich legen (Bild 6).

3. Die Assistenzperson nun die Stapel umordnen lassen, während Sie nicht hinschauen (Trick dadurch weniger durchschaubar) — dabei aber jeden Stapel jeweils so belassen wie er ist.

4. Die Assistenzperson drei Stapel auswählen lassen; dann alle anderen Kartenstapel einschl. der überschüssigen, siehe oben, in einem großen Stapel sammeln (Bild 7).

5. Die Person die oberste Karte auf zweien der drei verbliebenen Stapel wenden lassen (Bild 8).

Wenn Sie den Trick richtig ausgeführt haben, können Sie nun folgendermaßen herausfinden, welche Karte zuoberst auf dem letzten Kartenstapel liegt:

6. Die Werte der beiden gewendeten Karten addieren und danach IMMER 10 hinzuaddieren. Im Beispiel auf Bild 8 ergibt sich: 8 + 5 + 10 = 23. Nun aus dem großen Stapel von vorhin eine Anzahl Karten entsprechend der soeben durch Addition ermittelten Zahl entnehmen, hier also 23 Karten. Nun die noch verbliebene Anzahl Karten zählen. Die Anzahl der im Stapel verbliebenen Karten wird dem Wert der von Ihnen zu ‚erratenden‘ Karte entsprechen. Im Bild 8 ist diese Karte eine 6.

7. Geben Sie vor, ”erfühlen” zu können, welche Karte oben liegt. Nennen Sie Ihrer Meinung nach den Kartenwert und lassen Sie die Assistenzperson die Karte auf dem letzten Stapel aufdecken.

Die dem zweiten Kartentrick zugrundeliegende Mathematik

Obiger Trick funktioniert, weil errechenbar ist, wie viele Karten sich im letzten Stapel befinden. In unserem konkreten Beispiel liegt in den drei Stapeln jeweils folgende Anzahl Karten:
Im 5er-Stapel zählten wir bis 13, also 5, 6, 7, 8, 9, 10, 11, 12, 13. Dieser Stapel hat 13 – 4 = 9 Karten, und da auf den Zahlen 1, 2, 3 und 4 keine Karten liegen, können wir einfach 4 subtrahieren. Wir können also die Kartenanzahl durch Feststellen von 13 – 5 + 1 = 13 – 4 ermitteln. Wir addieren 1 zur Zahl auf der Karte hinzu, da auf der 5er-Karte ja eine Karte liegt.