Wenn die Rätsel zu verzwickt sind, kann die Mathematik unten auf der Seite weiterhelfen.
1. Herausforderung
Zeichne einen Umschlag, der aussieht, wie auf dem Bild gezeigt. Zeichne den Umschlag mit nur einer Linie, d. h.: Du hebst den Bleistift erst dann wieder an, wenn der Umschlag fertig gezeichnet ist. Es ist nicht erlaubt, die gleiche Linie zwei Mal oder mehrmals zu zeichnen. Wenn es beim ersten Mal nicht gelingt, dann versuche es einfach erneut – das gilt nicht als Schummeln.
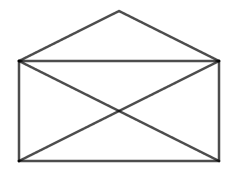
2. Herausforderung
Welche dieser Figuren kann nicht mit einer langen Linie gezeichnet werden?
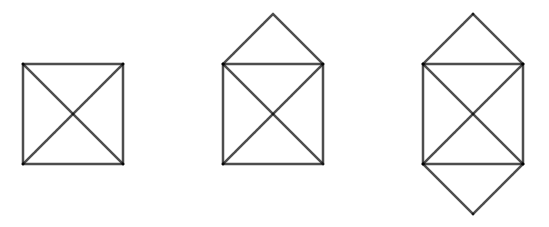
3. Herausforderung
Kann man bei dieser Figur eine lange Linie durch alle 16 Wände ziehen, sodass alle Wände genau einmal gekreuzt werden? Du bestimmst selbst, wo die Linie beginnt und endet.
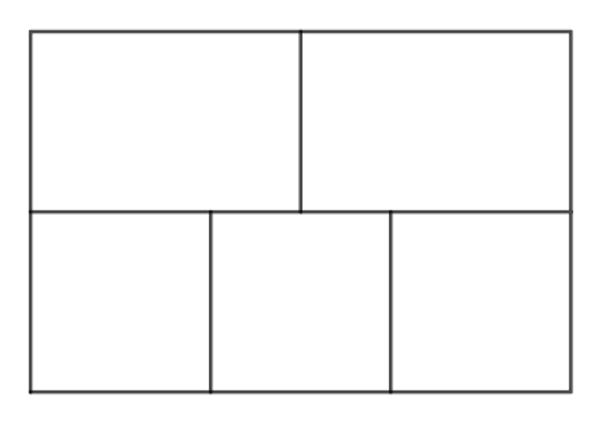
Die Mathematik hilft – Graphentheorie
Vielleicht kanntest Du die Zeichenaufgabe der 1. Herausforderung bereits, bei der es darum geht, einen Umschlag, wie den im Bild gezeigten, mit nur einer langen Linie zu zeichnen – und vielleicht kennst du sogar eine Lösung, die darauf basiert, dass zwei eindeutige Eckpunkte für den Anfang und das Ende der Linie erforderlich sind. Aber weißt Du auch, warum dies funktioniert? Mathematik kann dir helfen, diese Frage zu beantworten.

Hinweise für die Herausforderungen?
Zeichne einen Umschlag, der aussieht, wie auf dem Bild gezeigt. Zeichne den Umschlag mit nur einer Linie, d. h.: Du hebst den Bleistift erst dann wieder an, wenn der Umschlag fertig ist. Es ist nicht erlaubt, die gleiche Linie zwei Mal oder mehrmals zu zeichnen.
Kannst Du die Aufgabe lösen? Wenn Du es noch nicht versucht hast, dann probiere es einfach erst einmal aus, bevor Du weiterliest.
Es ist gut möglich, dass es funktioniert – manchmal geht es allerdings auch schief. Wo Du mit der Linie beginnst, ist wichtig – so viel können wir schon einmal verraten. Wenn Du in der Mitte einer Seite beginnst, wirst Du keinen Erfolg haben. Es ist also wichtig, in der richtigen Ecke zu starten. Aber wo ist die richtige Ecke?
Am besten ist es, wenn wir den Ecken Namen geben, damit wir sie unterscheiden können:
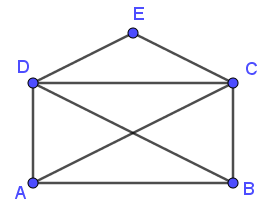
Zwei der Punkte sind gute Startpunkte. Bei den anderen drei wird jeder Versuch fehlschlagen – aber welche sind das, und warum?
Betrachten wir zunächst die Herausforderung. Wir müssen den Umschlag so zeichnen, dass wir dafür nur eine Linie verwenden, ohne den Bleistift anzuheben. Wir haben also nur eine einzige Linie, um zum Ziel zu kommen. Eine solche Linie kann unendlich viele Formen annehmen. Aber wie auch immer sie aussieht: die Linie hat genau zwei Enden – eines, an dem Du mit dem Zeichnen beginnst, und das andere, an dem Du damit endest. Wenn Du genau an derselben Stelle beginnst und endest, kann man jedoch die beiden Enden nicht sehen.
Und genau so muss dies bei der Lösung unserer Briefumschlag-Herausforderung sein: Die Linie hat genau zwei Enden!
Sehen wir uns die Ecken (A, B, C, D und E) des Umschlags genauer an. Die lange Linie hat verschiedene Knoten. Die Linie muss von einem Knoten zum nächsten geführt werden, bis der gesamte Umschlag fertiggezeichnet ist. Die kurzen Linien zwischen den Knoten nennen wir Kanten. Es gibt zum Beispiel eine Kante zwischen den Punkten B und D, aber keine Kante zwischen den Punkten A und E.
Wenn die Linie nur zwei Enden hat, müssen mindestens drei der fünf Knoten an einer Position liegen, an denen die Linie lediglich vorüberläuft, wobei diese Punkte weder der Anfang noch das Ende sind.
Stellen wir uns einen solchen Punkt vor, an dem die Linie weder beginnt noch endet. Die Linie erreicht den Punkt und wird fortgesetzt. Es gibt jetzt also zwei Kanten an diesem Punkt – eine, zu der die Linie hinläuft und eine, von der sie sich entfernt. Wenn die Linie dort noch einmal verläuft, haben wir vier Kanten an diesem Punkt. Und so werden jedes Mal, wenn die Linie den Punkt passiert, zwei Kanten hinzugefügt.
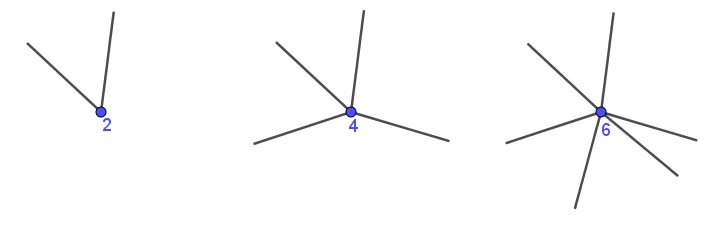
Auf diese Weise können wir die Anzahl der Kanten an jedem der Knoten zählen. Wir nennen diese Zahl die Valenz des Knotens. Knoten, bei denen die Linie nicht beginnt oder endet, haben, wie wir oben herausgefunden haben, immer eine Valenz, die eine gerade Zahl ist – eine gerade Valenz.
Ein Knoten, an dem die Linie beginnt oder endet, hat immer eine ungerade Valenz. In Fällen, in denen die Linie im selben Knoten beginnt und endet, muss die Valenz gerade sein – kannst Du erklären, warum?
Probiere einmal, die Valenz an den Knoten des Umschlags zu zählen. Hilft Dir das, festzustellen, welches die beiden richtigen Ausgangspunkte sind?
Es gibt Apps mit Spielen, die auf der Idee von Zeichnungen, die nur mit Linien ausgeführt werden, basieren. Wenn Du nach „One Touch Drawing“, „One Line“ oder ähnlichem suchst, wirst Du verschiedene Apps finden.
In einer App (One Touch Drawing) sieht die Umschlag-Herausforderung folgendermaßen aus: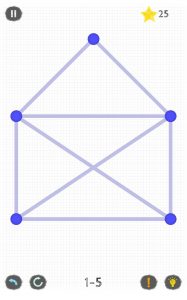
Eine andere App (1LINE) hat diese Variante: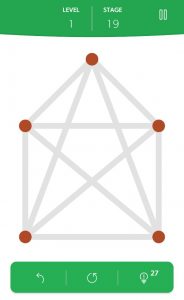
Links zu Apps:
One touch Drawing: iOS / Android
1LINE: iOS / Android
Kannst du die Variante lösen? Wenn Du deine Kenntnisse über gerade und ungerade Valenzen einsetzt: Welche der beiden Aufgaben ist Deiner Meinung nach am einfachsten zu lösen?
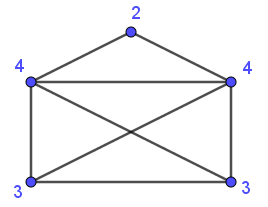
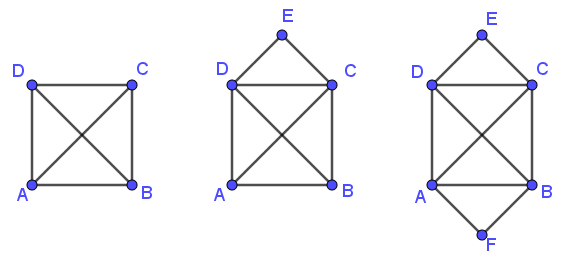
Mathematik hilft nicht nur, eine Lösung zu finde – man kann damit auch feststellen, ob es überhaupt eine Lösung gibt. Hier sind drei fast identische Aufgaben – bei der Aufgabe in der Mitte geht es um die bekannte Umschlag-Herausforderung. Aber was ist mit den anderen beiden? Können sie gelöst werden?
Und zum Schluss stellen wir Dir noch eine zusätzliche Herausforderung. Sie ist ein wenig anders gestaltet – aber vielleicht kannst Du ja dein Wissen über Valenz nutzen, um sie zu lösen?
Zusätzliche Herausforderung: Ist es möglich, eine lange Linie so zu zeichnen, dass alle Wände (16 Stück) in der Figur genau einmal von der Linie gekreuzt werden? Du kannst selbst bestimmen, wo die Linie beginnen und enden soll.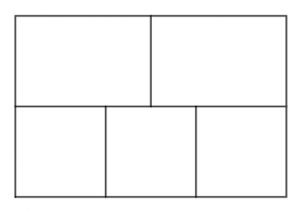
Hier wird an einer Lösung gearbeitet, aber die Linie muss noch einen Teil der Wände überqueren.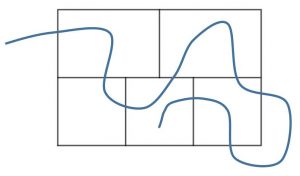
Ekstra Herausforderung:
Zuletzt eine Frage, die Du möglicherweise beantworten kannst, wenn Du Dein Wissen darüber nutzt, was Valenz ist und wie viele Enden eine Linie hat:
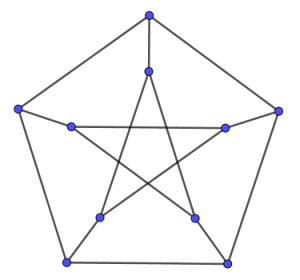
Die Zeitung, die du liest, ist Teil des Projekts MatKult, bei dem fünf Institutionen zusammenarbeiten. Wir haben deshalb eine Vorliebe für fünfeckige Figuren. Eine ganz besondere fünfeckige Figur ist der Petersen-Graph unten. Er kann nicht mit einer langen Linie gezeichnet werden. Wie viele verschiedene Linien musst Du mindestens zeichnen?

Können sie mir bitte die Lösung schicken ich habe alles versucht
Danke
Nicht alle Herausforderungen haben eine Lösung …