Der Name und die Person Elbridge Gerry sind dir vielleicht nicht bekannt, und dennoch ist er berühmt berüchtigt – nicht nur, weil er der 5 Vizepräsident der USA war, sondern vor allem für seine „kreative“ Einteilung der Wahlbezirke. Sein Name wurde zum Synonym für die Strategie, diese Einteilung ganz bewusst so vorzunehmen, dass ein bestimmtes Ergebnis erreicht wird. Ein solches Vorgehen wird heute als „Gerrymandering“ bezeichnet.

In der letzten Ausgabe von MatOnline haben wir uns in einigen Artikeln mit der Mathematik von Wahlen und dem 100. Jahrestag der Abstimmung zum Grenzverlauf zwischen Dänemark und Deutschland beschäftigt:
„In einer idealen Welt würde jede Wahl zwei Grundsätze erfüllen: Sie wäre frei und sie wäre gerecht. Jeder erwachsene Bürger hätte frei die Möglichkeit, eine Partei oder einen Kandidaten zu wählen, und jede einzelne Stimme hätte das gleiche Gewicht. Eine freie Wahl zu gewährleisten, ist die Aufgabe der Gesetzgebung und damit ein juristisches Problem. Aber was ist mit der Gewährleistung einer gerechten Wahl? … Die Mathematiker stießen sie auf zahlreiche Paradoxe und Überraschungen. Schon im Jahre 1785 bemerkte der französische Mathematiker Marquis de Condorect (1743–1794) ein Paradox in Wahlverfahren, die darauf beruhen, dass die Wähler bestimmten Kandidaten den Vorzug geben, woraufhin der Kandidat mit dem niedrigsten Ergebnis ausscheidet. Daraufhin wird das Verfahren wiederholt, bis einer der Kandidaten von mehr als der Hälfte der Wähler gewählt wird. … Der Marquis de Condorect stellte nun Folgendes fest: Wenn wir beispielsweise die drei Kandidaten A, B und C und drei Wähler haben, deren Wahl „A-B-C“, „B-C-A“ und „C-A-B“ lautet, gewinnt A vor B mit 2:1. Aber es gewinnen auch B vor C mit 2:1 und C vor A mit 2:1. Selbst wenn dieses Verfahren also sehr gerecht zu sein scheint, ist es nicht frei von Paradoxen.“ (Claus Michelsen)
Aber warum ist es so schwer, eine gerechte und freie Wahl durchzuführen? Nun, einmal wegen der oben genannten Paradoxe, aber eben auch wegen bewusst vorgenommener Änderungen, die sich auf ein Wahlergebnis auswirken können, wie es beispielsweise bei der Unterdrückung von Wählerstimmen der Fall ist. Letztendlich geht es hierbei nur um die menschliche Gier nach Macht. Im Jahre 1812 unterzeichnete Gerry, der Gouverneur von Massachusetts, ein Gesetz, das die Wahlbezirke im Staat veränderte. Einer dieser neuen Bezirke erinnerte viele an ein Monster oder einen Salamander,
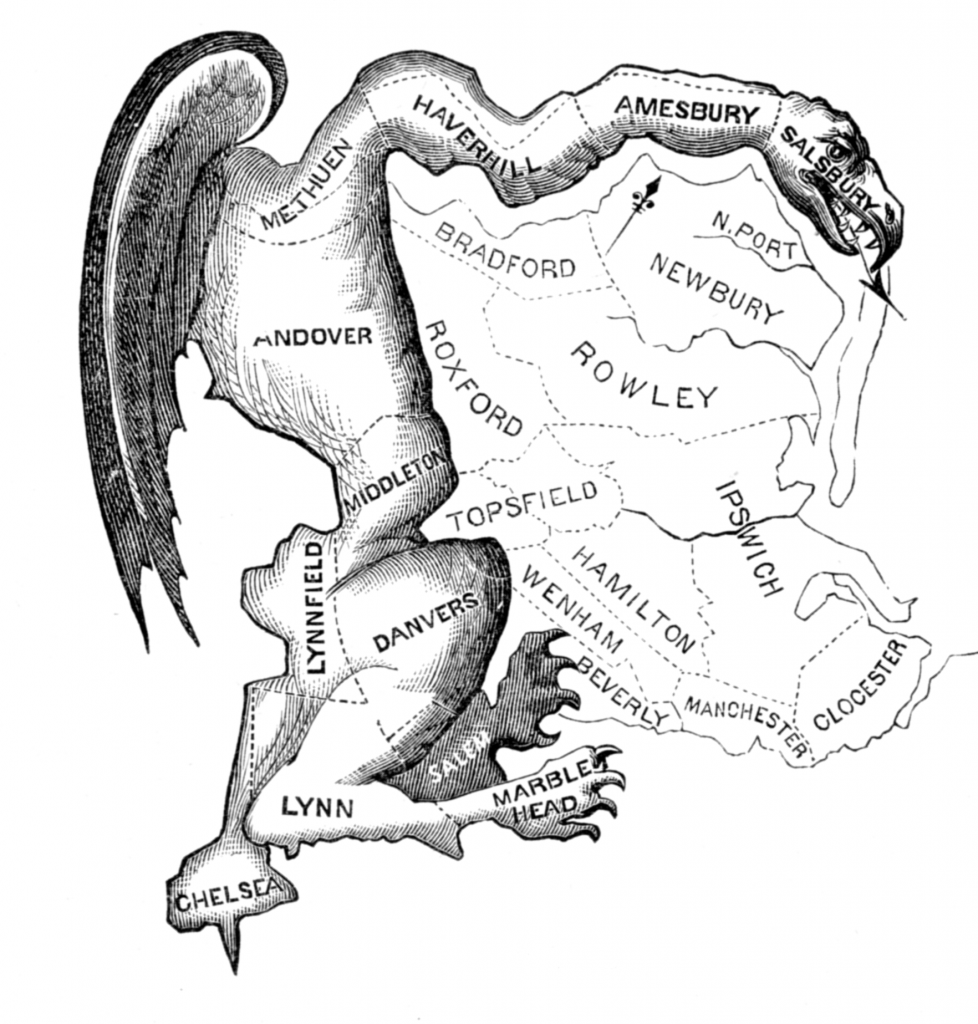
und so verschmolzen Gerry und der Salamander zu dem Wort, das wir heute kennen: Gerrymandering. Das Ziel des Gerrymandering besteht darin, die Bedeutung „deiner“ Stimmen zu stärken und diejenigen, die für einen anderen Kandidaten oder eine andere Partei abgegeben werden, ins Leere laufen zu lassen. In Massachusetts verlor Gerry zwar die dann folgende Wahl, aber seine Wahlbezirke trugen dazu bei, seiner Partei, der Democratic-Republican Party, auch weiterhin die Macht im Senat zu sichern.
Wie funktioniert Gerrymandering?
Ganz grundlegend gibt es zwei Methoden, um Wahlbezirke einzuteilen: die proportionale und die disproportionale. Nehmen wir einmal an, wir haben ein Gebiet von 5 x 10, in dem sich die Stimmen für die gelbe und die grüne Partei folgendermaßen verteilen:
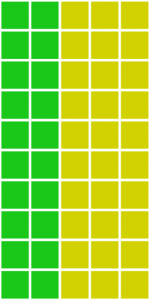
Es gibt 40 % grüne Felder und 60 % gelbe Felder. Stelle dir nun vor, dass das Gebiet von 5 x 10 in 5 Bezirke mit jeweils 10 Feldern eingeteilt werden soll. Bei der ersten Möglichkeit (proportional) versucht man, ein repräsentatives Ergebnis zu erreichen, bei dem die Stimmenaufteilung so ausgeglichen wie möglich ist. Das bedeutet, dass die 5 Bezirke nach Möglichkeit so eingeteilt werden, dass sie alle das tatsächliche Verhältnis repräsentieren (40/60), was zu folgendem Ergebnis führt:
5 Bezirke ⋅ 40 % = 2
Ausgehend von diesem Gedankengang würden die Grünen 2 und die Gelben 3 Bezirke gewinnen. Das kann auf verschiedene Arten geschehen, wie es beispielsweise hier gezeigt wird:
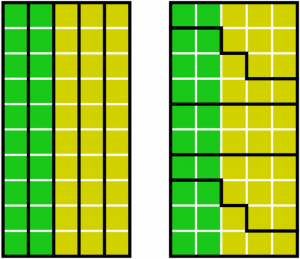
Die linke Verteilung ist sehr geradlinig und fasst alle „Gleichgesinnten“ zusammen, aber es kann eventuell die Gefahr bestehen, dass die Stimmprozentsätze/Beteiligung leiden, weil das Ergebnis von vornherein feststeht. Als Beispiel kann man hierfür unter anderem Bereiche wie Kalifornien und New York nennen, in denen die Demokraten bei der letzten Wahl sehr stark waren. Aber es gibt auch Nuancen. So kann man in New York in jeder Partei so genannte „ballot lines“ wählen, die für verschiedene Strömungen (Richtungen) innerhalb der Partei stehen, wie beispielsweise „Working Families“ in New York. Der rechte Kasten erbringt dasselbe Ergebnis, vermischt dabei jedoch die Stimmen, sodass die Wahlbezirke allesamt Stimmen beider „Parteien“ beinhalten.
Eine disproportionale Aufteilung könnte so aussehen

Sie ist so optimiert, dass die gelben Stimmen mehr Gewicht bekommen und Gelb in allen 5 Bezirken gewinnt. Selbst wenn die Wahl lokal in jedem Bezirk eine knappe Sache ist, spiegelt das endgültige Ergebnis nicht die Verteilung der einzelnen Stimmen wider. Es erinnert ein wenig an die „Winner-Takes-All“-Wahlsysteme, die wir im Artikel „Die deutsch-dänische Grenze 1920: Eine demokratische Wahl“ beschrieben haben:
„… wenn man mit der so genannten ‚Winner-Takes-All‘-Methode arbeitet, wie es bei der englischen Parlamentswahl der Fall ist. Bei dieser Methode entspricht jeder Wahlbezirk einem Mandat im Parlament, was bedeutet, dass die Wahl faktisch aus vielen kleinen Wahlen besteht, die keinen unmittelbaren Einfluss aufeinander haben. Das hat den Vorteil, dass jeder Bezirk eine sehr direkte Verbindung zum Parlament hat. Die Konsequenz ist aber auch, dass ein Wahlergebnis möglicherweise nicht besonders repräsentativ ist, wenn man den Blick auf das gesamte Land erweitert. So waren die Konservativen bei der letzten Wahl im Jahre 2019 die absoluten Gewinner, wenn man sich die Mandate ansieht. Dort errangen sie ein Plus von 14,8 %, aber ihr Stimmanteil lag nur 1,2 % höher als bei der vorigen Wahl. Die Labour-Partei hingegen verlor 22,5 % ihrer Plätze (Mandate) im Parlament, obwohl sie bei den Stimmen im Vergleich zur vorigen Wahl „nur“ ein Minus von 7,8 % verzeichnen musste. Ein Grund für diesen Unterschied könnte sein, dass die Labour-Partei einige Kopf-an-Kopf-Rennen verloren hatte, die die Konservativen für sich verbuchen konnten.“
Bei einer Wahl, bei der man im Hinblick auf die Einteilung der Wahlbezirke kreativ vorgeht, kann man die Macht so verschieben, dass sie letztlich nicht mehr widerspiegelt, wie wirklich abgestimmt wurde. Das kann man hier gut sehen:
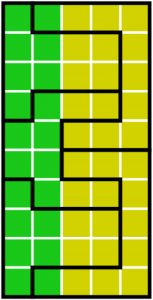
Die zwei Beispiele zur kreativen Bezirkseinteilung zeigen, dass man auf diese Weise zu einem nicht repräsentativen Ergebnis gelangt. Im ersten Fall übernimmt Gelb alle 5 Bezirke, obwohl sie „nur“ 3/5 oder 60 % der Stimmen bekommen. Im zweiten Fall bekommt Grün aufgrund der Einteilung einen zusätzlichen Bezirk, sodass sie 3/5 der Bezirke haben, aber nur 2/5 (40 %) der Stimmen. Die Einteilung der Bezirke ist also für das Ergebnis einer Wahl von großer Bedeutung.
Gerrymander-Index
Man kann einen Gerrymander-Index ansetzen, der auf der folgenden Formel beruht: Je unregelmäßiger die Form, desto höher der Index. Der Gerrymander-Index zeigt also nicht, warum ein Wahlbezirk so aussieht, wie er es tut, sondern nimmt nur Bezug auf die Form und verweist damit indirekt auf mögliche Verbindungen und eine kreative Einteilung der Wahlbezirke. Mehr Erklärungen zum Index bietet der in der Washington Post erschienene Artikel „America’s most gerrymandered congressional districts. Gerrymandering kann zu einigen interessanten Wahlbezirken führen:
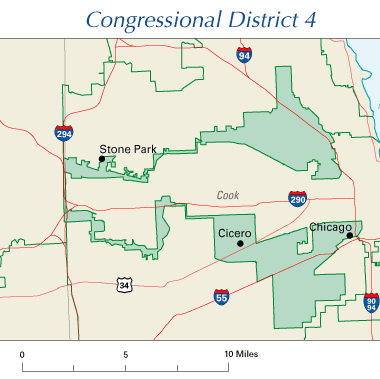
Achte hier nicht nur auf die Form, sondern auch darauf, dass es sich um einen zusammenhängenden Bezirk handelt (entlang der 294. Straße verläuft eine kleine, schmale grüne Linie).
Ein zusammenhängender Wahlbezirk in Maryland.
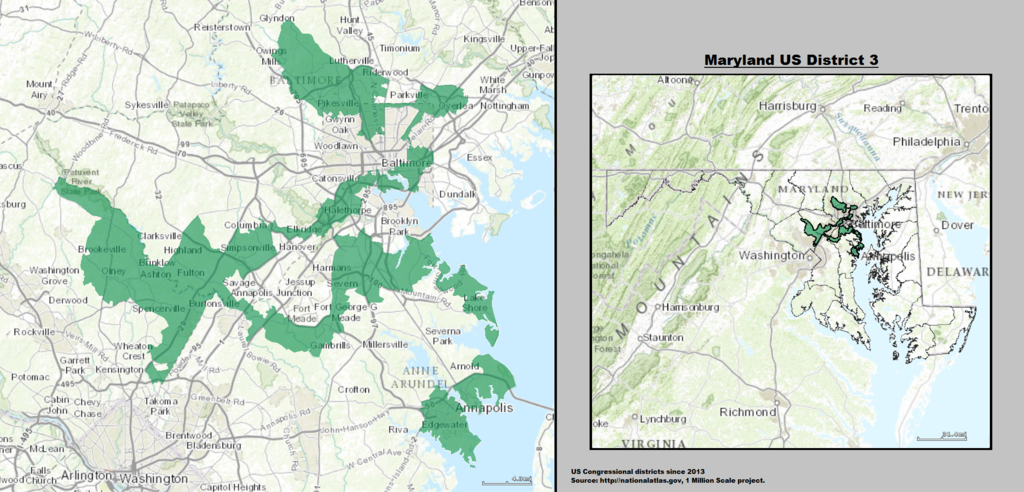
Ein zusammenhängender Wahlbezirk in Maryland.
Mehr über Gerrymandering erfährst du hier:

Gib den ersten Kommentar ab