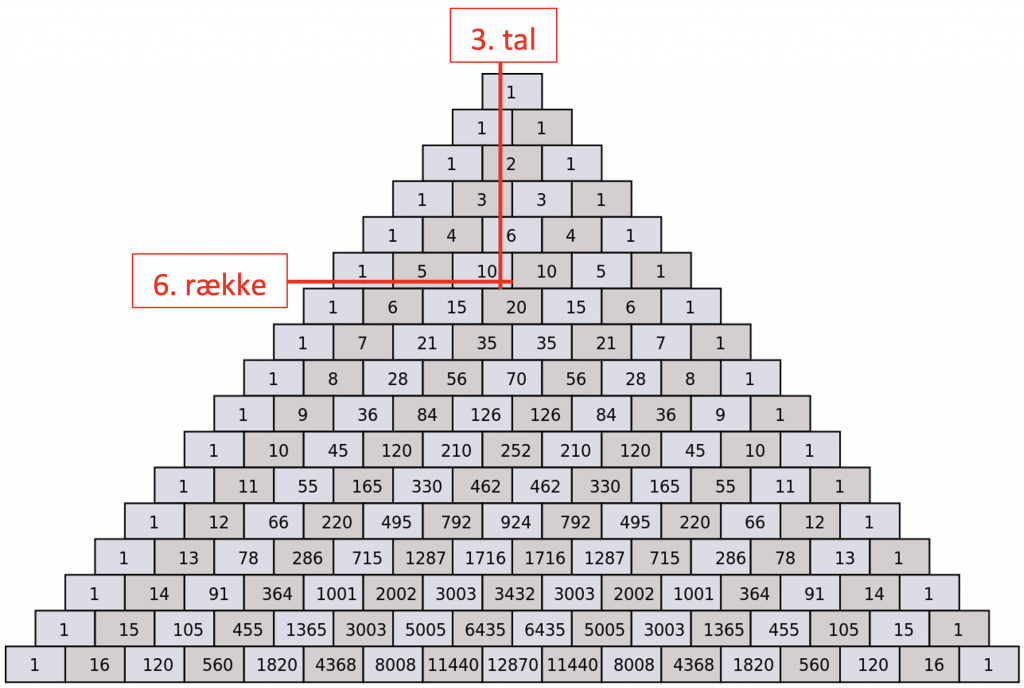
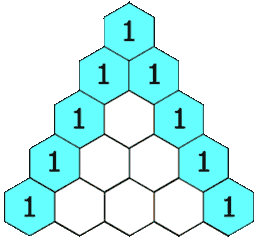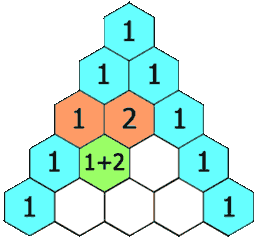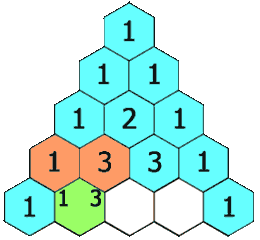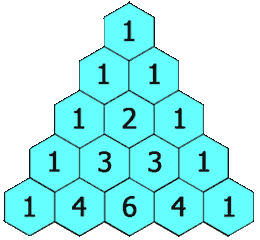
Die ersten sommerlichen Tage sind da, die Eissaison hat begonnen. Für viele heißt das: Her mit der guten alten Eiswaffel! Aber die Lieblingseisdiele hat 10 verschiedene Kugeln zur Auswahl, und Sie können sich nicht entscheiden, welche Kombination Sie für Ihr Eis mit zwei Kugeln wollen. Dann stellt sich die Frage. Wie oft muss ich den Sommer über die Eisdiele besuchen, um alle Kugeln in allen Kombinationen zu probieren? Diese Frage hat sich der Eistütenverkäufer nie gestellt, also kann er Ihnen da leider nicht helfen. Aber wie nicht anders zu erwarten, muss es doch einen mathematischen Weg geben, um das herauszufinden. Einfaches Nachschlagen wäre hier natürlich schöner als umständliches mathematisches (Be)Rechnen. Hier kommt das mathematische Konzept des „Pascalschen Dreiecks“ ins Spiel. Kurz erläutert, ist das Pascalsche Dreieck eine Pyramide mit einem Ziegelstein ganz oben mit der Zahl Eins. In der Reihe darunter sind zwei Steine, die beide die Zahl Eins tragen. In der nächsten Reihe befinden sich drei Ziegelsteine mit den Zahlen Eins, Zwei und Eins darauf. Die Zahl auf dem jeweiligen Ziegelstein ergibt sich aus der Addition der Zahlen der Steine in der darüberliegenden Reihe, die der Ziegelstein darunter berührt — zu sehen in der nebenstehenden Abbildung, in der eine solche Pyramide mit 17 Reihen gezeigt ist:
Ursprung und Anwendung des Dreiecks
Bevor wir sehen, wie diese spezielle Pyramide beim Eisproblem helfen kann, schauen wir uns die Ursprünge des Dreiecks und einige der mathematischen Geheimnisse an, die es birgt. Das Pascalsche Dreieck wurde von dem französischen Mathematiker und Physiker Blaise Pascal (1623-1662) erdacht. In seinem kurzen Leben gelangen Pascal mehrere bedeutende Entdeckungen sowohl in der Mathematik als auch in der Physik, wobei er heute am besten für die Einheit des Drucks (Pascal) bekannt ist, der er seinen Namen gab. Neben seiner Thematisierung von Druck, vor allem in Flüssigkeiten, leistete er auch Pionierarbeit im Bereich der Wahrscheinlichkeitsrechnung, und er erfand die erste Rechenmaschine. Seine Arbeiten zur Wahrscheinlichkeitsrechnung führten 1665 zur posthumen Veröffentlichung eines Werks mit dem Titel „Traité du triangle arithmetique“, das das Pascalsche Dreieck beschreibt. Das Dreieck war nicht nur bahnbrechend in dem Sinne, dass es zum ersten Mal für die mathematische Induktion[1] verwendet wurde, sondern es wurde auch zum Nährboden für viele andere mathematische Theorien. So ermittelt es u. A. die Koeffizienten bei der Berechnung von Quadrat- und Kubiksätzen, wie unten gezeigt:
[1] Die mathematische Induktion umfasst das mathematische Konzept, das mit dem Dominoeffekt gleichgesetzt werden kann. Es gibt einen Ausgangsschritt, bei dem der erste Dominostein fällt, und einen Induktionsschritt, bei dem der nächste Dominostein nach dem ersten Dominostein kippt. Dadurch kippen alle Steine der betreffenden Reihe.
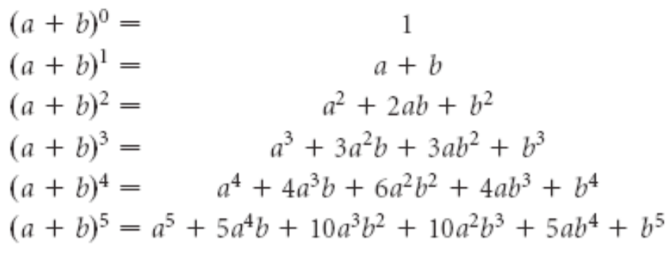
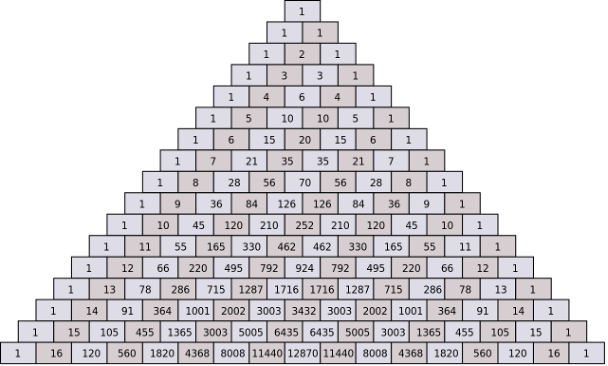
Der Aufbau des Dreiecks an sich ist einfach, da es nur das Addieren von zwei Zahlen erfordert, aber es kann mehrere mathematische Begriffe visualisieren, die viel ausgeklügelter sind als nur das Addieren von Zahlen. Einige dieser Begriffe sollen hier vorgestellt werden. Zunächst einmal sind alle Bausteine im Dreieck Binomialkoeffizienten, und hieraus ergibt sich die Verbindung zur Wahrscheinlichkeitsrechnung. Der Binomialkoeffizient 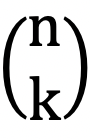 bezeichnet die Anzahl der Arten, auf die man ”k” verschiedene Elemente aus einem Bestand aus ”n” verschiedenen Elementen entnehmen kann. Dargestellt anhand des Pascalschen Dreiecks gibt ”n” die Nummer der Reihe beginnend mit Null an, d. h. Reihe eins hat die Nummer , Reihe zwei hat n = 0, Reihe zwei hat n = 1 osv. ”k” gibt die Zahlen von links nach rechts an, wiederum mit Null beginnend und dann aufwärts. Der Grundgedanke des Dreiecks ist somit, dass der Wert eines Binomialkoeffizienten sich durch Untersuchen des Ziegelsteins ermitteln lässt, der mit dem ”n”- und ”k”-Wert des Koeffizienten übereinstimmt. Sehen wir uns mal ein Beispiel an. Der Wert
bezeichnet die Anzahl der Arten, auf die man ”k” verschiedene Elemente aus einem Bestand aus ”n” verschiedenen Elementen entnehmen kann. Dargestellt anhand des Pascalschen Dreiecks gibt ”n” die Nummer der Reihe beginnend mit Null an, d. h. Reihe eins hat die Nummer , Reihe zwei hat n = 0, Reihe zwei hat n = 1 osv. ”k” gibt die Zahlen von links nach rechts an, wiederum mit Null beginnend und dann aufwärts. Der Grundgedanke des Dreiecks ist somit, dass der Wert eines Binomialkoeffizienten sich durch Untersuchen des Ziegelsteins ermitteln lässt, der mit dem ”n”- und ”k”-Wert des Koeffizienten übereinstimmt. Sehen wir uns mal ein Beispiel an. Der Wert 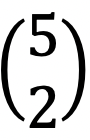 lässt sich durch Ermitteln der Reihe bestimmen, die n = 5, aufweist, also die sechste Reihe, da die erste ja die nullte Reihe ist. Danach sucht man die in der Reihe die die Zahl, die k = 2, aufweist, also die dritte Zahl von links, da wiederum die erste Zahl er k = 0 ist. Absolviert man diese Übung in dem abgebildeten Dreieck, so findet sich ein Ziegelstein mit der Zahl 10. Zur Bestätigung, ob bzw. dass dies korrekt ist, kann man die mathematische Formel aus der Tabelle verwenden:
lässt sich durch Ermitteln der Reihe bestimmen, die n = 5, aufweist, also die sechste Reihe, da die erste ja die nullte Reihe ist. Danach sucht man die in der Reihe die die Zahl, die k = 2, aufweist, also die dritte Zahl von links, da wiederum die erste Zahl er k = 0 ist. Absolviert man diese Übung in dem abgebildeten Dreieck, so findet sich ein Ziegelstein mit der Zahl 10. Zur Bestätigung, ob bzw. dass dies korrekt ist, kann man die mathematische Formel aus der Tabelle verwenden:

Es ist also erkennbar, dass die Theorie konsistent ist. Dies gilt für alle Werte im Pascalschen Dreieck. Die Konstruktion des Dreiecks besagt, dass ein Bausteinwert die beiden obigen Bausteinwerte addiert, was auch — wie in der Tabelle zu sehen — mit Binomialkoeffizienten ausgedrückt werden kann.
Diese Struktur kann für verschiedene Aspekte der Mathematik verwendet werden — dargestellt anhand eines Galtonbretts. Es handelt sich, wie abgebildet, um ein Brett mit einer Anzahl von Nägeln, durch die Kugeln hindurchlaufen können. Bei jedem Aufprall gegen einen Nagel kann sich die Kugel entweder links oder rechts um ihn herumbewegen und das Brett durchlaufen, um schließlich in einem der Fächer am unteren Ende des Bretts aufgefangen zu werden.
Obwohl es theoretisch zufällig ist, ob die Kugel links oder rechts um jeden Nagel herumläuft, lässt sich dennoch etwas über das Muster sagen, nachdem eine große Anzahl von Kugeln abwärts durch das Brett gewandert ist. Im Bild rechts ist eine blaue Linie eingezeichnet, die die Verteilung der Kugeln nach deren ‚Landung‘ zeigt. Diese Verteilung wird als Binomialverteilung bezeichnet und ist mit dem Pascalschen Dreieck verwandt. Wenn man eine Reihe im Pascalschen Dreieck nimmt und jedes Kästchen für ein Fach stehen lässt und die Zahl im Kästchen für die Anzahl der Kugeln in dem jeweiligen Fach stehen lässt, ergibt sich die gleiche Binomialverteilung wie auf dem Galtonbrett. Dies ist nur eines von vielen Beispielen dafür, wie Pascals Dreieck mit der Mathematik verbunden ist.
Um auf die Situation mit der Eisdiele zurückzukommen, haben wir ein Instrument, mit dem wir herausfinden können, wie oft man die Eisdiele im Sommer besuchen muss, um alle Kombinationen von Kugeln in einer Eistüte zu probieren. Wenn „n“ die Anzahl der verschiedenen Elemente angibt, aus denen man wählen kann, muss es 10 sein, da es 10 verschiedene Geschmacksrichtungen gibt. Das heißt, wir müssen die Zeile mit n=10 im Pascalschen Dreieck finden, und „k“ gibt die Anzahl der verschiedenen gewählten Geschmacksrichtungen an, nämlich 2 (wir erinnern uns). Das heißt wiederum, wir müssen uns die Zeile 11 des Dreiecks ansehen und die 3. Zahl von links finden, und damit wissen wir, wie oft wir die Eisdiele besuchen müssen. Nach einem kurzen Blick auf das Pascalsche Dreieck ergibt sich die Zahl 45, und wir können daraus folgern, dass es ein guter Sommer mit vielen Eistüten wird.
Verborgene Muster im Dreieck
Diese Mathematik beschreibt die Konstruktion des Pascalschen Dreiecks und wofür es eingesetzt werden kann, aber es gibt noch viele weitere mathematische Konzepte, die sich im Dreieck verbergen. Auf den ersten Blick erkennt man schnell, dass das Dreieck symmetrisch ist, und beim Betrachten der Diagonalen von oben nach unten erkennt man eine Zahlenfolge. In der zweiten Diagonale ist das z. B. 1, 2, 3, 4, 5, 6, …, die wir als die natürlichen Zahlen kennen. Aber welche Zahlenfolgen ergeben sich beim Betrachten der dritten und vierten Diagonale? Ein weiteres zu berücksichtigendes Element ist, ob es ein Muster in der Summe der Zahlen in jeder Zeile gibt. Stellen Sie hier mal entsprechende Überlegungen an und überprüfen Sie anhand der folgenden Tabelle, ob Sie richtig liegen. Sehen Sie sich auch andere Beispiele für verborgene Muster im Pascalschen Dreieck an, die Sie vielleicht ‚erforschen‘ möchten
Pascals Dreieck erzählt eine Geschichte davon, wie es, obwohl es in seiner Einfachheit sehr leicht zu konstruieren ist, große Mengen an Wissenschaft (ver)birgt, die in vielen verschiedenen Bereichen genutzt werden, etwa in der Wahrscheinlichkeitsrechnung in der Mathematik, der Spektroskopie in der Welt der Chemie und der genetischen Bestimmung im Bereich der Biologie.


Gib den ersten Kommentar ab