Dieser Beitrag ist eine ausführlichere Ausarbeitung einiger der im Artikel ”Matematiske sæbebobler” genannten Themen. Der Artikel ”Matematiske sæbebobler/Seifenblasen” thematisiert beispielsweise die vier mathematischen Regeln, denen Seifenfilm oder Seifenhaut und Seifenblase folgen. Die Regeln wurden von dem belgischen Physiker Joseph Plateau (1801-1883) formuliert. Es geht auch um die Frage, was für ”Abdrücke” Seifenblasen hinterlassen, wenn sie auf eine ebene Fläche, z. B. eine Tischplatte geblasen werden.
Hier eine Darstellung der beiden ”Seifenblasenabdrücke”, die 3 bzw. 4 Blasen gleicher Größe mit gemeinsamen Häuten oder ‚Wänden‘ auf einer ebenen Fläche erzeugen:
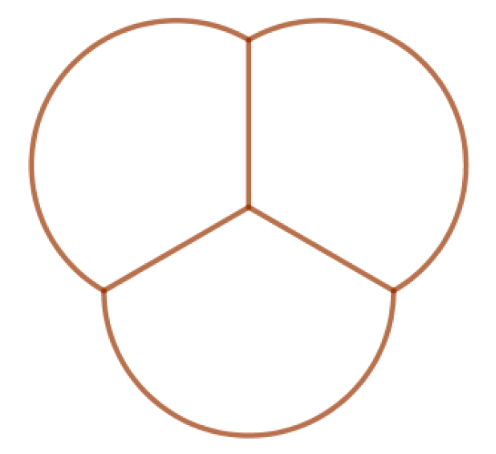
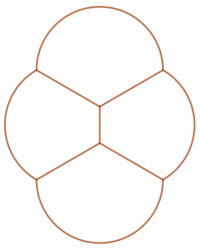
Seifenhäute bemühen sich immer um eine Minimierung ihrer Fläche (mehr dazu im ersten Artikel) und bilden daher Gruppen wie die Abdrücke in der obigen Zeichnung. Indem sie gemeinsame ‚Wände‘ haben, reduziert sich insgesamt ihre Oberfläche.
Versuchen Sie selbst, ob Sie die gleichen Abdrücke wie oben hinbekommen. Denken Sie daran, dass sich die ‚Bubbles‘ am besten auf die Tischfläche blasen lassen, wenn diese zuvor mit einem leicht ausgewrungenen Lappen befeuchtet wurde.
Das beste Werkzeug zum Ausblasen ist ein Strohhalm. Es kann schwierig sein, die Blasen zu kontrollieren, wenn man durch den kleinen Ring bläst, der oft beim Kauf einer kleinen Dose Seifenblasenwassers mitgeliefert wird. Hilfe zu einem Rezept für ein selbstgemachtes Seifenblasenbad und Werkzeuge zur Erzeugung von Seifenblasen finden Sie unter www.soapbubble.dk.
Als nächstes geht es im Beitrag um den Sonderfall, wenn zwei Blasen auf einer ebenen Fläche sich ‚Wand an Wand‘ aneinanderschmiegen, sich also eine gemeinsame ‚Wand‘ teilen. Anders als im ersten Teil des Beitrags soll es jetzt auch darum gehen, dass die beiden Blasen ggf. nicht gleich groß sind.
Aber eins nach dem anderen: So sieht zunächst der Abdruck bei gleicher Blasengröße aus, wenn also beide Blasen das gleiche Luftvolumen haben:
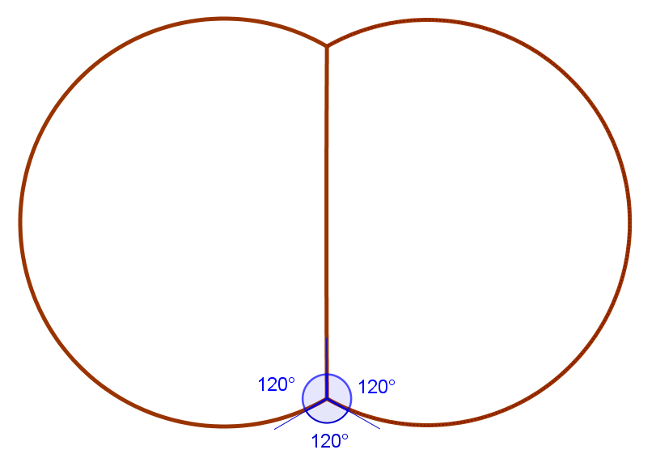
Versuchen Sie selbst, zwei Blasen gleicher Größe auf eine Tischplatte aufzubringen. Beachten Sie dabei besonders die gemeinsame ‚Wand‘ aus Seifenfilm und den Winkel, in dem sich die Blasen an den ‚Enden‘ berühren.
Betrachten wir die Zeichnung der beiden Seifenblasenabdrücke, so erkennen wir, dass die Blasen der dritten Regel von Plateau folgen: dass sich Seifenblasen immer in einem Winkel von 120° berühren (angegeben durch die blauen Winkel). Gilt das auch für die beiden Blasen, die Sie erzeugt haben?
Außerdem können wir erkennen wir, dass der Abdruck der gemeinsamen Wand zwischen den Blasen eine gerade Linie ohne Krümmung bildet. Oder wie der Mathematiker sagen würde; sie hat eine Krümmung gleich Null. Gilt das auch für Ihre Blasen?
Dass die gemeinsame Wand keine Krümmung hat, gilt nur in diesem speziellen Fall, in dem die beiden Blasen gleich groß sind. Wenn die Blasen unterschiedlich groß sind, herrscht im Inneren der Blasen nicht der gleiche Luftdruck. Und wenn der Luftdruck innerhalb der Blasen nicht gleich ist, wölbt oder drängt sich die Blase mit dem höheren Luftdruck in die Blase mit dem niedrigeren Luftdruck hinein.
Der Luftdruck im Inneren einer Seifenblase hängt im Allgemeinen von drei Dingen ab: dem Luftdruck in der Umgebung, der Oberflächenspannung und der Krümmung des Seifenfilms. Da uns hier nur die Druckdifferenz zwischen den Blasen interessiert, können wir den Umgebungsluftdruck ignorieren. Die Oberflächenspannung hängt nur von der verwendeten Seifenblasenflüssigkeit ab und ist daher in allen Seifenfilmhäuten konstant. In unserem Fall hier ist es also die Krümmung der Blasen, die bestimmt, ob sie den gleichen inneren Luftdruck haben. Und die Krümmung der einzelnen Blasen hängt davon ab, wie groß die einzelnen Blasen jeweils sind. Je größer die Blase, desto kleiner die Krümmung.
Der Luftdruck im Inneren der Blase wird durch die Oberflächenspannung des Seifenfilms verursacht. Die Oberflächenspannung bewirkt, dass die Blasen die kleinstmögliche Oberfläche suchen, d. h. sich zusammenziehen. Wenn sich eine Blase zusammenzieht, wird die Luft im Inneren der Blase komprimiert (verdichtet), wodurch der innere Luftdruck entsteht. Wie bereits erwähnt, hängt der Luftdruckunterschied zwischen den Blasen von deren Größe ab. Kleine Blasen sind stark gekrümmt und weisen damit einen relativ hohen Luftinnendruck auf, während eine große Blase eine kleine Krümmung und damit einen geringeren Luftinnendruck als die kleine(re) Blase hat.
Eine kleine Beobachtung, die Sie selbst machen können: Pusten Sie gegen Seifenblasen, die frei schweben. Kleine Blasen behalten eher ihre kugelförmige Form, größere Blasen können hingegen ihre Form verändern, aber wenn die Blasen aus dem starken Luftstrom herauskommen, werden sie wieder kugelförmig.
Wenn Sie wirklich große Blasen erzeugen, fällt es der Oberflächenspannung schwer, die Menge an Luft im Inneren der Blase zusammenzuhalten. Und selbst kleinste Bewegungen in der umgebenden Luft werden deutlich sichtbar auf den riesigen Seifenblasenfilm drücken.
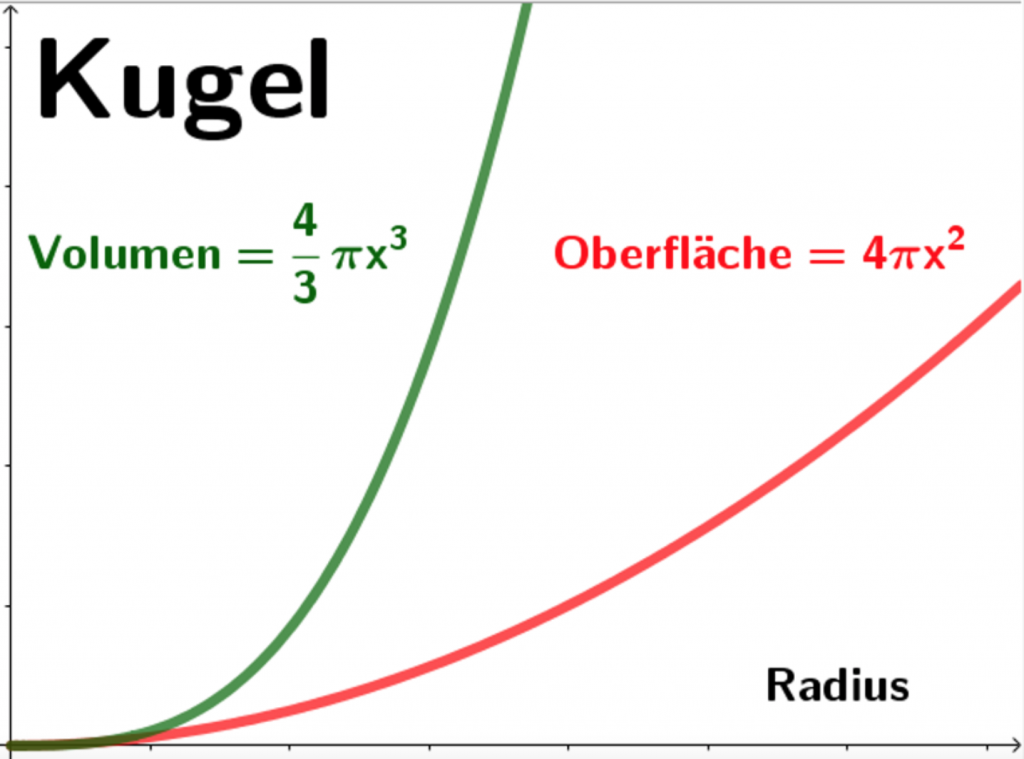
Die Darstellung mit den Kurven lässt erkennen, dass mit zunehmendem Radius einer Kugel der Rauminhalt (das Volumen) stärker zunimmt als die Oberfläche. Populär ausgedrückt, kann man sagen, dass die Oberflächenspannung der Verlierer ist, wenn es darum geht, die Luft innerhalb großer Blasen ruhig zu halten.
Beachten Sie die unterschiedlichen Blasengrößen im Bild unten. Die kleinsten Blasen halten die Kugelform am besten.


Zurück zu den beiden Blasen auf der Tischplatte. Was passiert, wenn die Blasen nicht gleich groß sind? Genau, die eine Blase wölbt sich leicht in die andere hinein, weil, wie oben erläutert, der Luftdruck in der kleineren Blase größer ist, weshalb die kleinere in die größere Blase hineindrängt.
Das könnte dann z. B. aussehen wie in den Bildern unten. Rechts sind die beiden Blasen gerade geplatzt, aber ihre „Abdrücke“ sind noch zu sehen:


Einen solchen Blasenabdruck können wir nun mathematisch mithilfe von Zirkel und Winkelmessgerät konstruieren. Wir brauchen dazu einen 60-Grad-Winkel. Haben Sie kein Winkelmessgerät zur Hand, so können Sie sich auch mittels eines Stück Papiers einen 60-Grad-Winkel ‚erfalten‘, und zwar so:
Nun ist es an der Zeit, die Blasenabdrücke zu konstruieren. Sie benötigen ein Blatt Papier, den Winkelmesser und einen Zirkel. Klicken Sie sich in der Animation unten Schritt für Schritt durch und arbeiten Sie unterwegs mit Zirkel und Lineal auf Ihrem Blatt Papier.
Die Animation ist dynamisch, Sie können also die blauen Punkte verschieben. Auf diese Weise können Sie Position und Größe der Blasenabdrücke verändern, müssen aber darauf achten, dass die drei roten Bogenteile am Ende innerhalb des Papiers liegen. Möglicherweise ist Ihre Papierversion auch zu groß für das Papiermaß; dann versuchen Sie es bitte erneut.
Am Ende könnte das Ganze dann so aussehen:


Aber passen Mathematik und Seifenblasen jetzt zueinander? Das werden wir überprüfen!
Legen Sie Ihren konstruierten Seifenblasenabdruck in einen Klarsichtkunststoffbeutel, z. B. einen Gefrierbeutel. Befeuchten Sie die Außenseite des Beutels, damit Sie Seifenblasen auf ihn pusten können.
Können Sie die Größe der beiden Blasen so anpassen, dass sie auf die von Ihnen gezeichneten Abdrücke passen? Be(ob)achten Sie dabei die gemeinsame Seifenfilmwand der Blasen.


Es gibt einen Zusammenhang zwischen den Krümmungen der beiden Blasen und der gemeinsamen Wand: Die Krümmung der großen Blase addiert mit der Krümmung der gemeinsamen Wand ist gleich der Krümmung der kleinen Blase — erkennbar in dieser Konstruktion: https://www.geogebra.org/m/n5KbBNpT
Sie haben nunmehr mathematisch Blasenabdrücke zweier Seifenblasen auf einer ebenen Fläche konstruiert, und Sie haben überprüft, dass die Seifenblasen sich tatsächlich mathematikkonform und den ersten vier Regeln Plateaus (siehe den ersten Artikel) entsprechend verhalten.
Wir hoffen, dass Sie sich in Zukunft an Seifenblasen nicht nur wegen ihrer ästhetisch ansprechenden Formen und Farben erfreuen, sondern auch wegen ihrer mathematischen Eigenschaften. Seien Sie hiermit ermutigt, weiter mit Blasenformen und Skulpturen zu experimentieren. Sie könnten zum Beispiel versuchen, einige der Plateauschen Körper zu konstruieren, vielleicht mit Anregungen durch das Video auf dieser Seite. Letzteres ist eigentlich eine Einführung in einen Mathekurs, aber es thematisiert kurz die Plateauschen Körper, und in der letzten Hälfte kommen die Seifenblasen ins Spiel.
Mehr zum Thema Krümmung
Die Krümmung einer ebenen Kurve an einem Punkt ist eine Zahl, die man erhält, indem man „misst“, wie groß der Kreis ist, für den an diesem Punkt „Platz“ ist. Die Krümmung ist dann Eins geteilt durch den Radius dieses Kreises. Die Krümmung ebener Kurven wird mit Vorzeichen berechnet. Wenn also die Krümmung am Punkt P positiv ist, dann ist die Krümmung am Punkt Q negativ. Wenn wir das Vorzeichen weglassen, ist die Krümmung im Punkt P kleiner als im Punkt Q, weil der Radius des Kreises im Punkt P größer ist als der Radius des Kreises im Punkt Q. Eine Gerade hat die Krümmung Null, weil ein unendlich großer Kreis hier Platz hätte: https://www.matematiksider.dk/soapbubbles.html
Haben wir Ihr Interesse an Mathematik und Seifenblasen geweckt? Dann hier ein paar Vorschläge für weitere Infos: https://www.matematiksider.dk/soapbubbles.html — siehe das Literaturverzeichnis unten auf der Seite. Auf diese beiden Bücher möchten wir besonders hinweisen:
- Soap Bubbles – Their colours and the forces which mold them von C. V. Boys, das hier auf Englisch gelesen werden kann, aber auch ins Deutsche und Dänische übersetzt worden ist
- The Science of Soap Films and Soap Bubbles von Cyril Isenberg (nur auf Englisch erhältlich)

Es ist eine verständliche, anschauliche und somit gelungene Darstellung. Ich habe wieder was dazugelernt. Danke