Den Fuß von Uwe Seeler (Nachbildung in Übergröße vor’m Hamburger Volksparkstadion) und „Der Ball ist rund — ist er das wirklich?“ haben wir schon an anderer Stelle thematisiert. Zunehmend in den Fokus im Fußball in den letzten Jahren sind die sogenannten erwartbaren Tore, die expected goals (xG) gerückt. Dabei geht es um die Ausarbeitung eines Modells zur Messung der ‚Qualität‘ von Abschlussversuchen (also Torschüssen oder Kopfballversuchen), es geht um die Wahrscheinlichkeit, dass ein Versuch (attempt) tatsächlich zu einem Tor führt. Abschlussversuche definieren sich auf einer Skala von 0 bis 100 % — die Wahrscheinlichkeit für ein Tor pro Chance –, wobei in der Regel eine Grenze bei 0,80-0,90 (80-90 %) Chance auf ein tatsächliches Tor angenommen wird. Grob gesagt, zeitigt eine Chance nah vor dem gegnerischen Tor einen höheren xG-Wert als weiter entfernt:
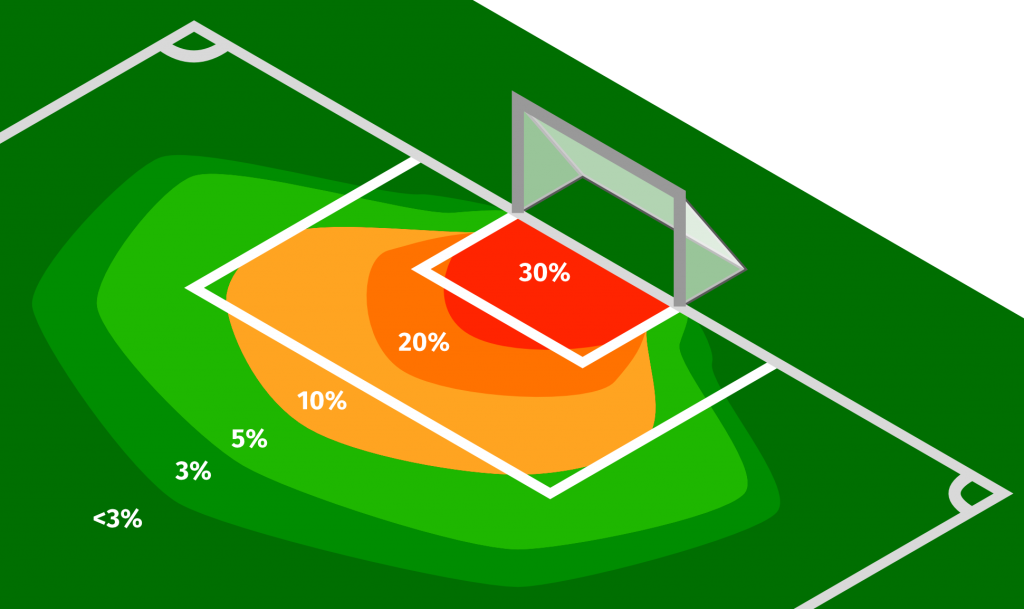
Hier sehen wir quasi eine ‚Wärmebildkameraaufnahme‘ davon, wo die Chancen am besten sind.
Außerdem geht es viel um die einzelnen Spieler, um die Fähigkeit der Mannschaft, Tore zu erzielen (mit Blick auf frühere Spiele) usw. Da gibt es beim Erstellen eines xG-Modells viele Parameter zu messen und zu berücksichtigen, und im Grunde ist es der Versuch zu veranschaulichen, wie sehr eine Situation das Potenzial hat, zu einem Tor zu führen. Deshalb trifft das System auch nicht immer ins Schwarze — einfach, weil xG in erster Linie lediglich versucht, eine Vorstellung von der Größe der auftretenden Chancen zu geben. Bei der Modellierung gibt es Fallstricke, und hinsichtlich xG kann es Situationen geben, z. B. ein Elfmeter, Eckball oder Freistoß, in denen der Torwart den Ball abwehrt, und ein anschließender freier Ball, etwa ein Abpraller, zu einer zweiten Chance führt. In der Realität ist nur 1 Tor pro Situation möglich, da das Spiel nach einem Tor vom Anstoßpunkt in der Platzmitte neu angepfiffen wird. Denkbar ist z. B. folgende Situation:
Elfmeter: 0,80 Torwahrscheinlichkeit
Folgechance: 0,70 Torwahrscheinlichkeit
Ergebnis: 1,50 Torwahrscheinlichkeit
Ein Modell muss also eine ‚Idee‘ davon haben, ‚wann‘ eine Situation vorbei ist, denn man kann hier nicht einfach unkritisch Prozentsätze addieren. Andernfalls könnte das oben beschriebene Problem auftreten, dass wir jeden Schuss als eine Torchance betrachten, in Wirklichkeit sind die beiden Situationen aber miteinander verbunden. Sie können hier mehr über dieses Problem lesen und wie xG es durch einen zusätzlichen Schritt berücksichtigt:
The maths behind this particular situation is as follows.
— The xG Philosophy (@xGPhilosophy) July 21, 2020
(1 - 0.78) x (1 - 0.90) = n
0.22 x 0.10 = 0.02
So there’s a 2% probability that Man City don’t score either chance.
Therefore:
1 - 0.02 = 0.98(xG)
So Man City should be awarded 0.98(xG) for this attack.
(5/6)
Kurz gesagt, beträgt im obigen Beispiel die Torwahrscheinlichkeit xG 0,94 und nicht 1,50:
Elfmeter + (1 – Elfmeter) · Folgechance =
0,80 + (1 – 0,80) · 0,70 = 0,94 Torwahrscheinlichkeit in der Situation
Das System greift jede Chance auf und versucht, sie aufgrund vieler Aspekte zu quantifizieren: Wo entsteht die Chance, wie ist der Winkel zum Tor, wer schießt, wie viele Tore hat man in der Vergangenheit erzielt, wie viele Spiele wurden absolviert u. v. a. m. Weitere Informationen dazu findet man hier: https://oneshortcorner.wordpress.com/2016/03/06/football-analytics-part-four-expected-goals/
Modelle für erwartbare Tore (expected goals)
Es ist nicht klar, was jedes Modell enthält, aber wir können versuchen, unser eigenes zu erstellen. Es ist jedoch ein vereinfachtes und beruht auf einer Situation und nicht auf einem Spiel:
Lionel Messi bekommt den Ball außerhalb des ‚Sechzehners‘ (das ist der Strafraum), umspielt einen Gegner und zieht ab!
Aber geht sein Schuss ins Tor?
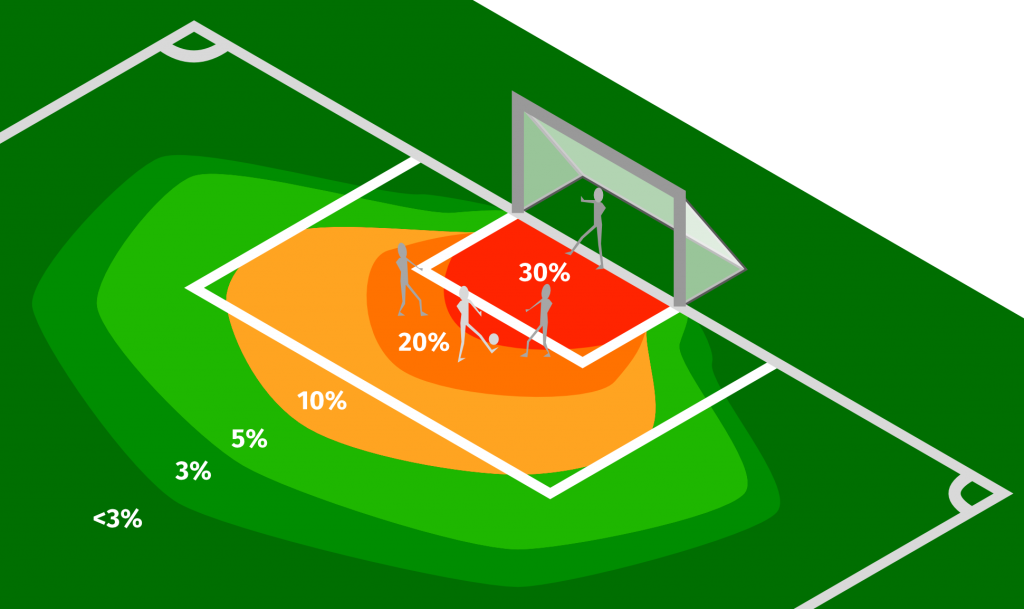
Sehen wir uns ein simples Torwahrscheinlichkeitsmodell an, bei dem wir einige Faktoren berücksichtigen:
[(Position des ballführenden Spielers) + (Winkel zum Tor)] · [(zu erwartende Tore des Spielers pro Spiel/pro Chance) · (Tore pro Abschlussversuch der Mannschaft)] – [Torwart – Abwehr] · (Faktor, wie viele Tore die Mannschaft erwartbar pro Torschuss ‚kassiert‘) =
(0,30 + 0,20) · (0,028 [vgl. 1,4 Tore/50 Abschlussversuche, OneShortCorner] · 25)
– (0,1 – 0,1) · 0,95 = 0,35 Torwahrscheinlichkeit
In unserem Modell würden wir also in mehr als einem Drittel der Fälle, in denen diese Situation eintritt, ein Tor erwarten. Hinter einem ‚echten‘ xG-Modell stehen eine Menge Daten, wobei Statistiken — wie z. B. wie viele Tore Messi pro 50 Schüsse erzielt — die Messung einzelner Situationen untermauern. Dieses Modell ist einfach, aber wenn Sie sich selbst an einem ‚echten‘ xG-Modell mit mehr Elementen versuchen möchten, dann sehen Sie sich dieses dreiteilige YouTube-Video an: https://www.youtube.com/watch?v=bpjLyFyLlXs
Wir können unser Modell schnell erweitern, indem wir prüfen, ob eine Mannschaft zu Hause mehr Tore erzielt als auswärts, den Schiedsrichter mitberücksichtigen, wie viele gelbe Karten ein direkter Gegenspieler hat und viele weitere Faktoren.
Wir müssen überlegen, wann eine Situation endet, damit wir einen konkreten xG-Wert für jede Chance in einem Spiel haben. Im Allgemeinen betrachtet xG dies pro Schuss — allerdings ist eine zusätzliche Berechnung erforderlich, wenn kurz danach eine weitere Chance eintritt, wie bei dem Elfmeter-Beispiel vorhin. Somit kann sich ein xG-Wert im Nachhinein ändern; und überhaupt sind einzelne Situationen viel einfacher zu berechnen als ein ganzes Spiel mit vielen Unwägbarkeiten, 22 Spielern, 3-5 Schieds- und Linienrichtern, 2 Trainern und Zuschauern. Wie man sieht, kann das Modell schnell sehr komplex werden.
xG ist auf Vieles anwendbar, wird aber oft mannschaftsintern genutzt, um zu analysieren, wo das Team und der Einzelne am besten Tore erzielen, wie und wann Chancen entstehen. Die Frage ist, ob man die Anzahl der Tore überhaupt vorhersagen kann.
Mehr zum Thema expected goals hier:
https://towardsdatascience.com/a-guide-to-expected-goals-63925ee71064

Gib den ersten Kommentar ab