Die Mathematik ist vielleicht nicht das erste, was dir in den Kopf kommt, wenn du eine Seifenblase siehst, aber tatsächlich benimmt sich eine solche Seifenblase ausgesprochen mathematisch. Wenn man „mathematisch“ denn so versteht, dass sie einigen bestimmten Regeln folgt, die wir mit Hilfe der Mathematik beschreiben können.
Wir interessieren uns nicht besonders für die Blasen als solche, sondern für den Seifenfilm, aus dem sie bestehen. Ein einfaches Beispiel für einen solchen Seifenfilm ist das, was du im Blasring siehst, kurz bevor du die Seifenblase in die Welt hinaus pustest. Die meisten Blasringe sind flach und damit zweidimensional, was bedeutet, dass der Seifenfilm, der sich in dem Ring aufspannt, ebenfalls flach ist.
Aber ein Seifenfilm muss nicht immer flach sein. Wenn der Rahmen, in dem er sich spannt, nicht flach und zweidimensional ist, ist auch der Seifenfilm nicht flach.
Hier siehst du drei Bilder eines Seifenfilms, der eine Art Rohr formt, das sich zwischen zwei runden Blasringen aufspannt.
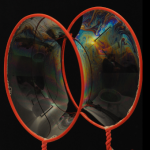
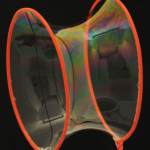
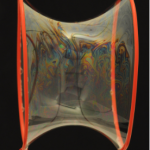
Diese Rohrform, die der Seifenfilm hier zeigt, nennt sich Katenoid. Beachte, dass das Rohr in der Mitte schmaler wird. Die Rohrform ist die Form, in der die Oberfläche eines zwischen zwei Ringen aufgespannten Films so gering wie möglich ausfällt. Der Seifenfilm nimmt diese Form ganz von selbst ein*. Wir werden hier nicht tiefer in die physikalische Erklärung einsteigen, sondern uns bloß merken, dass Seifenfilme die Eigenschaft haben, ihre Oberfläche zu minimieren. Das ist übrigens auch genau der Grund, weshalb Seifenblasen kugelrund werden. Denn die Kugel ist die Form, bei der die Oberfläche im Verhältnis zum Volumen am kleinsten ist.
Wenn du selbst einen katenoidförmigen Seifenfilm erschaffen möchtest, halte die beiden Ringe nah beieinander, wenn du sie aus dem Seifenwasser ziehst. Mit einem trockenen Finger bringst du den Seifenfilm, der sich in den zwei Ringen bildet, zum Platzen. Danach kannst du die Ringe vorsichtig voneinander weg bewegen. Wenn der Abstand zwischen den Ringen klein ist, kann man nur schwer erkennen, dass das Rohr in der Mitte schmaler ausfällt, aber wenn der Abstand größer wird, ist das deutlicher zu sehen. Achte darauf, die Ringe nicht zu weit voneinander zu entfernen. Ansonsten wird das Katenoid überdehnt und zerbirst in zwei flache Seifenfilme und eine kleine Blase. Wie groß der Abstand ist, den du zwischen die Ringe bringen kannst, bevor das Katenoid zusammenbricht, ist vom Radius der Ringe abhängig. Der Maximalabstand beträgt 4/3 des Radius. Das ist in etwa der Abstand, den die Ringe auf dem oben dargestellten Bild haben. Den faszinierenden Zusammenbruch eines Katenoids kannst du dir hier einmal in Zeitlupe ansehen: https://www.youtube.com/watch?v=mziis4pbBOw.
Zurück zu den mathematischen Regeln, denen die Seifenfilme folgen. Es war der belgische Physiker Joseph Plateau (1801–1883), der 1873 nach sorgsamen Experimenten mit Seifenfilmen vier Regeln erkannte und formulierte. Sie konnten erst im Jahre 1976 von Jean Taylor bewiesen werden. Und so lauten die vier Regeln – sie werden später im Text noch näher erläutert:
- Seifenfilme bestehen aus komplett glatten Flächen.
- Die mittlere Krümmung in einem Teil des Seifenfilms ist an jedem Punkt dieses Teils des Seifenfilms stets konstant.
- Seifenfilme treffen immer zu dritt in einem Winkel von cos-1(-1/2) = 120° aufeinander und bilden dabei die Plateau-Kante.
- Plateau-Kanten treffen immer zu viert mit einem Winkel von cos-1(-1/3) ≈ 109,5° aufeinander.
Sehen wir uns die vier Regeln etwas genauer an.
Regel 1 besagt, dass ein Seifenfilm glatt und gleichmäßig ist. Das ist so zu verstehen, dass er keine Kerben und Knicke aufweist (außer beim Zusammentreffen mit einem anderen Seifenfilm, aber dazu kommen wir in Regel 3 und 4).
Regel 2 besagt, dass sich ein Seifenfilm in seiner Gänze gleich krümmt, wenn man die mittlere Krümmung nimmt.
| Faktenbox: Was ist die mittlere Krümmung? |
|---|
Stelle dir vor, dass du auf einem Punkt der Erdoberfläche stehst und nach vorne/hinten sowie nach links/rechts blickst und untersuchst, wie stark sich die Erdoberfläche in beiden Richtungen auf- und abwärts krümmt. Stehst du auf dem Gipfel eines Hügels, krümmt sie sich in beiden Richtungen nach unten, aber stehst du auf dem Grund eines Kraters, dann krümmt sie sich in beiden Richtungen nach oben. Stehst du hingegen auf einem Fußballplatz, krümmt sie sich weder auf- noch abwärts.
Die mittlere Krümmung ist ein Maß, das besagt, wie stark sie sich an genau dem Punkt, an dem du stehst, insgesamt auf- oder abwärts krümmt. Bei dem Punkt auf der Hügelkuppe sagt man, dass eine positive mittlere Krümmung vorliegt. Am Kratergrund hast du eine negative mittlere Krümmung. Und auf dem Fußballplatz ist die mittlere Krümmung bei null.
Stelle dir nun vor, dass du mitten auf einem Bergpass stehst. Hier krümmt sich die Oberfläche in die eine Richtung aufwärts und in die andere Richtung abwärts. Die mittlere Krümmung hier auf dem Bergpass liegt daher bei (nahezu) Null. Damit die mittlere Krümmung bei genau Null liegt, musst du auf einem „mathematisch sauberen“ Bergpass stehen – denk daran, dass Seifenfilme immer mathematisch saubere Flächen bilden ☺
Die genannten Positionen sind auf den Abbildungen weiter unten rot gekennzeichnet (mit Ausnahme des Fußballplatzes, aber den kannst du dir sicherlich auch gut selbst vorstellen): Bilder von (die rote Markierung wurde hinzugefügt):
 |
Zurück zu Regel 2. Stelle dir beispielsweise eine einzelne Seifenblase vor, die rundherum gleich rund ist. Eine kleine Blase ist stark gekrümmt, während die Krümmung bei einer großen Blase nur gering ist. In beiden Fällen ist die Krümmung über die gesamte Blase hinweg gleich – ganz egal, wo dein Ausgangspunkt ist. Ein wenig überraschend erscheint vielleicht, dass die mittlere Krümmung bei dem oben erwähnten Katenoid ebenfalls an allen Punkten gleich ist. Kannst du erkennen, dass die Krümmung an jedem Punkt des Katenoids auf- und abwärts gerichtet ist?
Bei den Blasen ist die Krümmung auf jeder Seite über die gesamte Fläche hinweg gleich. Ein Ei hingegen wäre ein Beispiel für eine Form, die Regel 2 nicht entspricht. Denn ein Ei ist zwar eine Fläche, aber es ist an der einen Seite stärker gekrümmter (spitzer) als an der anderen, weshalb die mittlere Krümmung nicht an allen Punkten gleich ist, wie es Regel 2 vorschreiben würde.
Regel 3 besagt, dass immer da, wo sich drei Blasen treffen, jeweils zwei Blasen eine gemeinsame Oberfläche bilden und diese insgesamt drei Oberflächen in einer Kante (Plateau-Grenze) aufeinander treffen, bei der zwischen allen drei gemeinsamen Oberflächen ein Winkel von 120° zu beobachten ist. Sieh dir das Bild auf der rechten Seite an, das drei senkrechte Oberflächen mit grünem Boden und weißer Oberseite zeigt, die sich mit je 120° um die kleine, hellgrüne Grenze in der Mitte anordnen. Sie ist gelb schraffiert. Kannst du die 120° an den weißen Grenzen selbst entdecken?
Regel 4 besagt, dass diese Kanten (Plateau-Grenzen) zwischen den Seifenblasen immer zu viert aufeinandertreffen. Der Winkel von cos-1(-1/3) ≈ 109,5° ist dir vielleicht nicht gleich ein Begriff, aber es ist der Winkel, der entsteht, wenn du 4 Zahnstocher so in eine Kastanie steckst, dass sie so weit wie möglich voneinander entfernt sind. Auf dem Bild weiter unten treffen sich die drei weißen Grenzen und die kleine hellgrüne Grenze in der Mitte der vier Blasen (durch einen gelben Kreis gekennzeichnet).
Auf dem Bild sind vier Blasen. Drei „Tischblasen“, die auf der Unterlage aufliegen, und eine vierte, die auf den drei anderen ruht. Auf dem rechten Bild sind die Grenzverläufe mit Farben eingezeichnet. Dunkelgrün: Grenzflächen zur Unterlage. Hellgrün: Grenzflächen von der Unterlage aufwärts. Weiß: Innere Grenzflächen zwischen zwei „Tischblasen“ und der vierten Blase. Rot: Äußere Grenzflächen zwischen einer Tischblase und der vierten Blase.
Es ist nicht gerade einfach, gute Bilder von Blasen zu machen, um mit ihnen Regel 3 und Regel 4 zu illustrieren. Deshalb empfehlen wir dir wärmstens, selbst ein paar Seifenblasen zu pusten. Die beiden Regeln sind in der Wirklichkeit sehr viel leichter „in Augenschein zu nehmen“.
Sehen wir uns nun etwas näher an, wie die mittlere Krümmung aus Regel 2 im Falle des Katenoids zu verstehen ist. Stelle dir vor, dass du nicht auf einem Hügel, in einem Krater oder auf einem Bergpass stehst, sondern auf einem Katenoid. Suche dir deinen Punkt auf einem dieser Katenoide hier aus:
Drehe dich so, dass die Krümmung abwärts gerichtet ist, wenn du nach vorne siehst. Auch bei einem Blick nach hinten geht die Krümmung in exakt der gleichen Stärke abwärts. Wenn du dich nach links und rechts drehst, verläuft die Krümmung in dieser Richtung ebenso stark, nur andersherum – aufwärts statt abwärts.
Generell gilt: Bei einer Drehung um 90° hat die Krümmung in der neuen Richtung die gleiche Stärke wie zuvor, nur eben mit einem anderen Vorzeichen. Und das trifft für alle Punkte auf dem Katenoid zu. Das bedeutet, dass die mittlere Krümmung an allen Punkten des Katenoids Null ist. Flächen, die diese Eigenschaft haben, werden Minimalflächen genannt. Sieh dir weiter unten einmal an, wie du mit Seifenfilmen verschiedene Minimalflächen erzeugen kann, indem du die Form deines Blasrings veränderst.
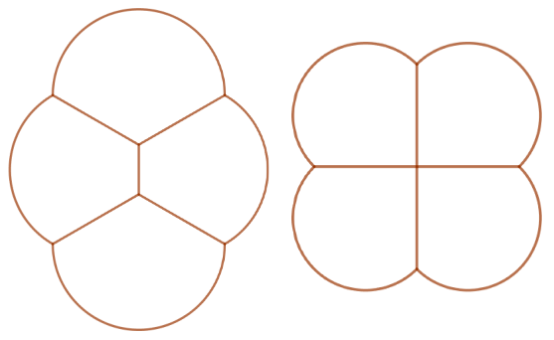
Du kannst selbst mit Seifenblasen experimentieren und mit eigenen Augen feststellen, dass Seifenfilme den vier Regeln von Plateau folgen. Versuche beispielsweise einmal, Seifenblasen auf einen Tisch zu pusten (der Seifenwasser aushalten kann). Feuchte den Tisch zunächst mit einem leicht ausgewrungenen Tuch an. Du kannst versuchen, die Seifenblasen wie diese Seifenblasenfußspuren aussehen zu lassen. Eine dieser Spuren ist unmöglich nachzupusten – findest du heraus, welche das ist?:
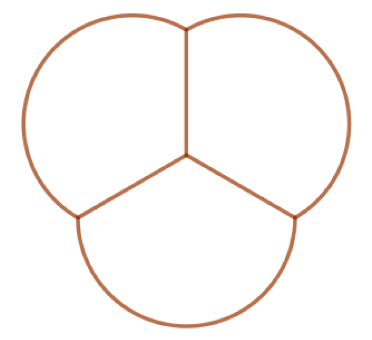
Wenn du schon dabei bist, Seifenblasen auf einen Tisch zu pusten, ist dies hier auch ein schönes kleines Experiment – ein Seifenblasentrampolin oder Katapult: https://www.youtube.com/watch?v=GWvlfddSOVQ. Im Video kannst du dir außerdem Beispiele zu den Plateau-Grenzen ansehen, die in Regel 3 und 4 erwähnt werden.
Ein weiterer einfacher Seifenblasenversuch besteht darin, einen eigenen Blasring zu basteln. Dafür eignet sich beispielsweise ein Kleiderbügel aus Draht oder ein Stück festes Stromkabel. Beginne mit einem Ring, aber versuche auch ruhig einmal, den Ring zu verdrehen, und achte dabei auf die Krümmung, die der Seifenfilm im Inneren deines Blasrings bekommt. Hier sind ein paar Vorschläge zu Formen, die du deinem Blasring geben kannst. Mit dem letzten kannst du einen Seifenfilm zaubern, der wie ein Möbiusband aussieht. Wenn sich im Blasring keine Blasen befinden (bei denen es sich ebenfalls um Seifenfilm handelt, nur eben mit Lufteinschlüssen), ist der Seifenfilm, auf den du blickst, eine Minimalfläche:
Hier findest du verschiedene Beispiele für Versuche mit geometrischen Blasen: https://soapbubble.dk/artikler/former (Dänisch) https://www.soapbubble.dk/en/articles/former (Englisch)
Benötigst du ein Rezept für Seifenblasenwasser oder andere Tipps zum Thema Seifenblasen, wirf einen Blick auf. www.soapbubble.dk – die Seite ist auf Dänisch und auf Englisch verfügbar
* Generell wird ein Seifenfilm immer versuchen, seine Oberfläche zu minimieren. Das liegt an der Oberflächenspannung des Seifenfilms. Wenn du mehr über die Oberflächenspannung und Seifenblasen erfahren möchtest, wirf einen Blick auf diese Seite: https://www.soapbubble.dk/artikler/overfladespaending (Dänisch) https://www.soapbubble.dk/en/articles/overfladespaending (Englisch)
https://www.researchgate.net/publication/233331312_Shape_and_curvedness_analysis_of_brain_morphology_using_human_fetal_magnetic_resonance_images_in_utero
Katenoide und die Seifenblasenfußspur sind von Soapbubble.dk
Die sonstigen Bilder sind eigene Produktionen
Gib den ersten Kommentar ab