Det er måske ikke matematik, du først tænker på, når du ser en sæbeboble, men faktisk opfører sæbebobler sig meget matematisk. Forstået på den måde, at de følger nogle bestemte regler, som vi kan beskrive ved hjælp af matematik.
Vi interesserer os ikke særligt for boblerne som sådan, men for de sæbehinder boblerne består af. Et simpelt eksempel på en sådan sæbehinde er den, der er i sæbeboblejernet, når du lige skal til at blæse en boble. De fleste sæbeboblejern er flade og som sådan todimensionelle, derfor bliver sæbehinden inde i sæbeboblejernet også flad.
Sæbehinder er dog ikke altid flade. Hvis den ramme hinden er spændt ud mellem ikke er flad og todimensionel, så bliver sæbehinden ikke flad.
Her er tre billeder af en sæbehinde som danner en slags rør mellem to runde sæbeboblejern.
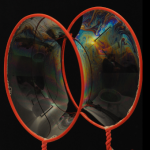
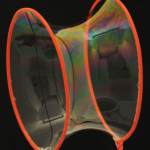
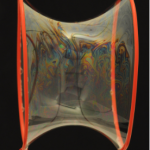
Den rørform som sæbehinden her laver kaldes en katenoide. Læg mærke til, at røret er smallere på midten. Rørformene er den form, der har det mindst mulige overfladeareal for en hinde spændt ud mellem de to ringe. Sæbehinden indstiller sig helt af sig selv på den måde*. Her går vi ikke nærmere ind i den fysiske forklaring, men hæfter os blot ved at sæbehinder har denne egenskab, at de minimerer deres overfladeareal. Det er for øvrigt derfor, at sæbebobler bliver kuglerunde. Kuglen er den form, der har den mindste overflade i forhold til volumen.
Hvis du selv vil lave en katenoideformet sæbehinde, så hold de to ringe tæt sammen, når du tager dem op af sæbeboblevandet. Med en tør finger sprænger du sæbehinden, der er inde i de to ringe. Herefter kan du tage de to ringe forsigtigt fra hinanden. Når afstanden mellem ringene er lille, er det svært at se, at røret er smallere på midten, men efterhånden som afstanden øges bliver det nemmere. Men pas på, kommer ringene for langt fra hinanden bliver katenoiden trukket over og danne to flade sæbehinder og en lille boble. Hvor langt ringene kan trækkes fra hinanden før katenoiden kollapser afhænger af radius på de to ringe, største afstand er 4/3 gange radius. Det er cirka den afstand, der er mellem ringene på billederne ovenfor. Du kan se det fascinerende kollaps af en katenoiden i slowmotion her: https://www.youtube.com/watch?v=mziis4pbBOw.
Tilbage til de matematiske regler, som sæbehinderne følger. Det var den belgiske fysikker Joseph Plateau (1801-1883), der i 1873 indså og formulerede de fire regler på baggrund af omhyggelige eksperimenter med sæbehinder. Først i 1976 blev de bevist af Jean Taylor. De fire regler lyder sådan – de forklares nærmere længere nede i teksten:
- Sæbehinder består af hele glatte flader.
- Middelkrumningen på en del af sæbehinden er altid konstant i ethvert punkt på den samme del af sæbehinden.
- Sæbehinder mødes altid tre i en vinkel på cos-1(-1/2) = 120° og danner herved en kant kaldet en Plateaurand.
- Plateaurander mødes i fire i en vinkel på cos-1(-1/3) ≈ 109.5°.
Lad os undersøger de fire regler lidt nærmere.
Regel 1 siger, at en sæbehinde er pænt og ensartet, forstået på den måde, at den er uden hakker og knæk (med mindre den mødes med en anden sæbehinde, men det kommer vi til i regel 3 og 4).
Regel 2 fortæller, at målt med middelkrumning, så krummer en sæbehinde på den samme måde over det hele.
| Faktaboks: Hvad er middelkrumning? |
|---|
Forestil dig, at du står et sted på jordoverfladen og kigger i retningen frem/tilbage samt retningen højre/venstre og undersøger, hvor meget jordoverfladen krummer op og ned i to retninger. Står du på en bakketop krummer det ned i begge retninger, men hvis du står i bunden af et krater, så krummer det op i begge retninger. Står du til gengæld på en fodboldbane, så krummer det hverken op eller ned.
Middelkrumningen er et mål for hvor meget det samlet set krummer op og ned set fra lige det punkt, hvor du står. Punktet på toppen af bakken siges at have en positiv middelkrumning, punktet i bunden af krateret har en negativ middelkrumning og punktet på fodboldbanen har en middelkrumning på nul.
Forestil dig nu, at du står lige midt i et bjergpas. Her krummer det op i den ene retning og krummer ned i den anden. Middelkrumningen her i bjergpasset er derfor (tæt på) nul. For at middelkrumningen bliver præcist nul, så skal det være et ”matematisk pænt” bjergpas – bemærk, at sæbehinder altid laver matematisk pæne flader.
De nævnte positioner er vist med en rød prik på tegningerne nedenfor (bortset fra fodboldbanen, men den kan du nok godt forestille dig):
 |
Tilbage til regel 2. Tænk fx på en enkelt sæbeboble, den er rund på samme måde over det hele. En lille boble krummer meget, mens en stor boble krummer lidt. I begge tilfælde er krumningen den samme på hele boblen uanset hvilket punkt du tager udgangspunkt i. Lidt overraskende er det måske, at middelkrumningen på katenoiden ovenfor er også den samme i alle punkter. Kan du få øje på, at det krummer både op og ned uanset hvor på katenoiden, du kigger?
I en klase af bobler er krumningen på hver af siderne i boblerne den samme over det hele. Et æg er et eksempel på en form, som ikke opfylder regel 2. Et æg er en flade, men ægget er mere krumt (spidst) i den ene ende end i den anden ende og derfor er middelkrumningen ikke den samme i alle punkter, som regel 2 ellers foreskriver.
Regel 3 siger, at når tre bobler mødes, så har boblerne to og to en fælles væg og disse i alt tre vægge mødes i en kant (en Plateaugrænse), hvor der er 120° mellem hver af de tre fælles vægge. Se billedet til højre, hvor der er tre lodrette vægge med grøn bund og hvid top, som er fordelt med 120° rundt om den lille lysegrønne grænse i midten. De har en gul skravering. Måske du selv kan få øje på andre 120° omkring de hvide grænser?
Regel 4 fortæller, at disse kanter (Plateaugrænserne) mellem sæbebobler altid mødes fire af gangen. Vinklen på cos-1(-1/3) ≈ 109.5° er måske ikke lige kendt, men det er den vinkel der opstår, hvis du stikker 4 tændstikker i en kastanje således, at tændstikkerne sidder så langt fra hinanden som muligt. På billedet nedenfor, mødes de tre hvide grænser og den lille lysegrønne grænse i midten af de fire bobler (markeret med en gul cirkel).
På billedet er fire bobler. De tre ”bordbobler”, som ligger på bordet, mens den fjerde hviler oven på de tre andre. På billedet til højre er grænserne tegnet op med farver. Mørkegrøn: Grænser, som er på bordpladen. Lysegrøn: Grænser, som går fra bordet og op. Hvid: Indre grænser mellem to ”bordbobler” og den fjerde boble. Rød: Ydre grænser mellem en bordboble og den fjerne boble.
Det er ikke nemt at tage gode billeder af bobler, så det er nemt at illustrere regel 3 og regel 4. Så derfor en stor opfordring til selv at blæse nogle sæbebobler. De to regler er meget nemmere at ”få øje på” i virkeligheden.
Lad os kigge lidt nærmere på hvordan middelkrumning fra regel 2 skal forstås i tilfældet katenoiden. Forestille dig nu, at du hverken står på en bakke, i et krater eller i et bjergpas, men at du står på en katenoide – vælg selv et punkt på af en af katenoiderne her:
Drej dig, så det krummer nedad, når du kigger frem. Så vil det krumme det præcis lige så meget nedad, hvis du kigger bagud. Hvis du så drejer dig mod højre eller venstre, så krummer det præcis ligeså meget i den nye retning, men bare den anden vej, altså opad i stedet for nedad.
Generelt gælder det, at hvis du drejer dig 90° så har krumningen i den nye retning præcis samme størrelse som før, men bare med det modsatte fortegn. Og dette gælder i alle punkter på katenoiden. Det betyder, at middelkrumningen i alle punkterne på katenoiden er nul. Flader, der har denne egenskab kaldes for minimalflader. Se nedenfor hvordan du kan lave forskellige minimalflader med sæbehinder ved at ændre formen på dit sæbeboblejern.
Du kan selv lave forsøg med sæbebobler og se, at sæbehinderne følger Plateaus fire regler. Prøv for eksempel at blæse bobler på et bord (der kan tåle sæbevand). Gør først bordet fugtigt med en let opvredet klud. Du kan prøve om du kan få boblerne til at efterligne disse boblefodspor – et af dem er umuligt, men hvilket?:
Når du er i gang med at blæse bobler på et bord, så er dette også et fint lille eksperiment – en sæbebobletrampolin eller katapult: https://www.youtube.com/watch?v=GWvlfddSOVQ. I videoen kan du også få øje på eksempler på de Plateaugrænser, som der nævnes i regel 3 og 4.
Et andet simpelt bobleforsøg er at lave sit eget sæbeboblejern af fx en renseribøjle eller et stykke stiv elektrikkerledning. Start med en ring, men prøv så at vride ringen og læg mærke til hvilken krumning, som sæbehinden får inde i sæbeboblejernet. Her et par forslag til former på sæbeboblejernet – med den sidste er det muligt, at lave en sæbehinde formet som et Möbisbånd. Hvis der ikke er bobler (altså sæbehinder, der indkapsler luft) i sæbeboblejernet, så er den sæbehinde du kigger på en minimalflade:
Se flere eksempler på forsøg du kan lave med geometriske bobler her: https://soapbubble.dk/artikler/former (dansk) https://www.soapbubble.dk/en/articles/former (engelsk)
Har du brug for en opskrift på sæbeboblevand eller andre sæbebobletips, så se evt. www.soapbubble.dk – siden findes både på dansk og engelsk
* Generelt vil en sæbehinde altid søge at minimere sit overfladeareal. Det skyldes overfladespænding i sæbehinden. Hvis du vil læse mere om overfladespænding og sæbebobler, så læs evt. her: https://www.soapbubble.dk/artikler/overfladespaending (dansk) https://www.soapbubble.dk/en/articles/overfladespaending (engelsk)
Kateniode og boblefodspor er fra Soapbubble.dk
Start debatten med en kommentar