Har du prøvet at blive snydt af et korttrick? Hvis ja, så er du måske blevet udsat for lidt matematisk magi. Mange korttricks bygger netop på matematik og kan forklares med enkle matematiske sammenhænge, tælling og logik.
Når du har læst denne artikel, så vil du kende 2 korttricks og de bagvedliggende matematiske sammenhænge. Du vil forhåbentlig også selv blive i stand til at udføre korttrickene og på den måde udføre matematisk magi!
Gode råd! Når du laver et korttrick, er det vigtigt, at du ikke afslører, hvordan og hvorfor tricket fungerer. Hvis du i stedet kan aflede din tilskuer ved at tale hele tiden, lave store armbevægelser, sige en trylleformular – Hokus Pokus, flødeboller med kokos – eller lignende, så vil dit trylletrick opleves mere magisk. Inddrag gerne din tilskuere ved at lade ham eller hende blande kortene og give valg undervejs, hvor det er muligt. På den måde vil dit trick blive mere uigennemskueligt, da det vil se ud som om, at du ikke har styr på alt, hvad der sker igennem tricket, men selvfølgelig har du det!
Det første korttrick
Når du udfører dette korttrick, vil du kunne gætte, hvilket kort en tilskuer har valgt mellem 21 tilfældige kort. Dette blot ved hjælp af lidt matematisk magi.
Hvad skal du bruge?
– 21 forskellige spillekort
– En tilskuer, som du kan lave korttricket med
Hvad skal du gøre?
1. Giv en tilskuer bunken med de 21 kort.
2. Bed tilskueren om at vælge et af kortene uden at fortælle eller vise dig hvilket.
3. Bed tilskueren om at blande bunken med de 21 kort og giv den herefter til dig.
4. Læg de 21 kort med billedsiden opad i tre kolonner med 7 kort i hver (se billede 1)
5. Spørg tilskueren: ”I hvilken kolonne ligger kortet, du valgte?”
6. Saml de tre kolonner af kort i tre bunker (se billede 2)
7. Læg de tre bunker oven på hinanden med bunken med det valgte kort i midten (se billede 3)
8. Gentag 4. til 7. trin 2 gange mere.
Hvis du har lavet tricket rigtigt, så vil det valgte kort nu ligge som det midterste kort i bunken af kort. Da der er 21 kort, vil det være det 11. kort i bunken. Du kan afslutte korttricket på mange forskellige måder, da du jo allerede nu ved, hvilket kort der er det rigtige. HUSK hele tiden at holde øje med, hvor kortet er! Du kan fx:
10a. Blot tælle fra bunkens top eller bund til kort nummer 11 og derefter afsløre kortet.
10b. Lægge kortene som blomster (se billede 4) og lade din tilskuer pege på de blomster, der skal enten blive eller fjernes. Du siger fx: ”Peg på blomsterne til højre eller blomsterne til venstre”. Hvis tilskueren peger på blomsterne med det rigtige kort iblandt, fjerner du de andre. Hvis tilskueren peger på de andre blomster, fjerner du dem, så det rigtige kort hele tiden bliver på bordet. Herefter deler du blomsterne i to nye samlinger, som tilskueren kan vælge imellem og fortsætter på samme måde, indtil der kun ligger det rigtige kort tilbage, som så afsløres.
Matematikken bag det første korttrick
Du behøver egentlig ikke at kunne forstå matematikken, som ligger bag tricket, for at kunne udføre det, men måske du alligevel er nysgerrig – Hvorfor virker det egentlig, og kan vi være sikre på, at det virker hver gang? Hvorfor det virker kan visualiseres på følgende måde:
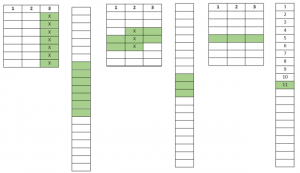
Når du lægger kortene op i de tre kolonner, og tilskueren afslører, i hvilken kolonne kortet ligger, så får du viden om, i hvilken del af kortene det valgte kort er iblandt. I det konkrete tilfælde kolonne 3 – de grønne (1).
I den næste del af tricket skal du samle de tre kolonner til tre stakke af kort. Stak nummer 3 lægger du nu i midten (2).
Når kortene igen lægges op i de tre kolonner, vil de mulige kort fordele sig i dem alle tre. Du beder nu tilskueren om at pege på den kolonne, hvor det valgte kort ligger, og du vil på den måde indskrænke de mulige kort til 2-3 forskellige kort. Hvis tilskueren peger på kolonne 1 eller 3, vil det være et af de 2 grønne kort, der er i den valgte bunke. Hvis tilskueren peger på kolonne 2, så vil det være et af de 3 grønne kort. Vi kigger her på det tilfælde, hvor det valgte kort ligger i kolonne 2, men det kunne selvfølgelig lige så godt have været en af de andre kolonner (3).
Kortene samles nu igen med den valgte bunke i midten. I det konkrete tilfælde får vi af tilskueren af vide, at kortet ligger i kolonne 2, hvorfor der nu er tre mulige kort tilbage, som ligger midterst i bunken (4).
Når du igen lægger kortene ud i tre nye kolonner, så vil de tre midterste fordele sig i de tre kolonner, så de ligger netop i midten i hver kolonne. Vi beder derefter vores tilskuer om at pege på kolonnen med det valgte kort, og der er nu kun ét muligt kort (5).
Når vi nu samler kortene igen og lægger bunken med det rigtige kort i midten igen, vil kortet nu ligge præcis midt i bunken som kort nummer 11. Dette uanset om det lå i 1., 2. eller 3. kolonne.
Dette trylletrick kan derfor forklares ved hjælp af netop enkle matematiske sammenhænge, tælling og logik.
Det andet korttrick
Når du udfører dette korttrick, så vil du kunne gætte, hvilket kort der ligger med bagsiden op, blot ved hjælp af lidt matematisk magi. Du kan desværre ikke sige noget om den kulør, kortet har, men kun hvilket tal der er på kortet, eller om det er en knægt (svarer til 11), dame (svarer til 12) eller konge (svarer til 13).
Hvad skal du bruge?
– Et helt spil kort. Det er vigtigt, at der er 52 kort, så du skal sikre dig, at der ikke mangler nogen
– En tilskuer, som du kan lave korttricket med
Hvad skal du gøre?
Du skal startede med at fordele alle kort i bunker på følgende måde:
1. Læg det første kort på bordet med forsiden opad. Tæl videre fra den værdi, der står på kortet og op til 13. Læg et kort oven på det første kort, hver gang du siger et nyt tal. Fx lægger du en 4er op med forsiden opad og tæller 5, 6, 7, 8, 9, 10, 11, 12 og 13. Nu vil der ligge 9 kort oven på din 4er (se billede 5). Herefter vendes bunken, så bagsiden er opad.
2. Lav bunker som i pkt. 1, indtil der ikke er flere kort tilbage. Hvis der er kort i overskud, hvor der ikke kan tælles op til 13, så samles de i en bunke for sig selv (se billede 6).
3. Lad nu din tilskuer flytte rundt på bunkerne, mens du vender ryggen til for at gøre tricket mindre gennemskueligt. Dog uden at tilskueren må ændre på bunkerne.
4. Lad nu din tilskuer om at vælge 3 bunker ud, og saml alle de andre bunker af kort inkl. de kort, der var i overskud, i en stor bunke (se billede 7).
5. Nu skal din tilskuer vende det øverste kort på to af de tre bunker, der er tilbage (se billede 8).
Har du lavet tricket rigtigt, så kan du nu finde ud af, hvilket kort der ligger øverst i den sidste bunke af kort på følgende måde:
6. Læg tallene på de to vendte kort sammen og læg derefter ALTID 10 til. I eksemplet på billede 8 giver det: 8 + 5 + 10 = 23. Tag nu den store bunke af kort fra før og tæl det antal, du fik ved at lægge de to tal sammen plus 10. I dette tilfælde 23 kort. Tæl nu antallet af kort, der er tilbage. Antallet af kort, der er tilbage i bunken, vil være af samme værdi, som der står på det kort, som du gerne vil gætte. På billede 8 er dette kort en 6er.
7. Lad som om, du kan ”føle dig frem til”, hvilket kort der ligger øverst. Fortæl din tilskuer, hvilket tal du mener står på kortet og lad tilskueren vende det øverste kort i den sidste bunke.
Matematikken bag det andet korttrick
Ovenstående trylletrick virker, fordi vi kan regne os frem til, hvor mange kort der er i den sidste stak. I det konkrete eksempel er der følgende antal kort i de tre bunker:
I 5er-bunken har vi talt op til 13, altså 5, 6, 7, 8, 9, 10, 11, 12, 13. I denne bunke ligger der 13 – 4 = 9 kort, og da der ikke ligger et kort på tallene 1, 2, 3 og 4, kan vi blot trække 4 fra. Vi kan altså finde antallet af kort ved at finde 13 – 5 + 1 = 13 – 4. Vi må lægge 1 til tallet på kortet, da der jo ligger et kort på tallet 5[LF1] .
[LF1]Kort er ental, så det tyske Card er fint

I 8er bunken har vi talt op fra 8 til 9, 10, 11, 12 og 13. I denne bunke ligger der således 13 – 8 + 1 = 13 – 7 = 6 kort.
Vi kan nu regne ud, hvor mange kort der er i den sidste stak og på den måde gætte tallet på kortet. Vi prøver først med det konkrete eksempel fra før, og derefter prøver vi at generalisere.
I bunken med de fjernede kort kan jeg tælle 29 kort. Jeg har vendt en 5er og en 8er, og jeg skal altid trække 10 ekstra fra, så må tallet på det sidste kort være: 29 – 5 – 8 – 10 = 6 (se billede 9 & 10), men hvorfor skal vi egentlig trække 10 fra?
For at kunne forklare dette, kalder jeg tallet på de tre øverste kort i bunkerne for bogstaver.
a er tallet på det øverste kort i den første bunke af kort
b er tallet på det øverste kort i den anden bunke af kort
c er tallet på det øverste kort i den tredje bunke af kort, som vi ikke kender
I bunken med de fjernede kort er der:
52 – (13 – a + 1) – (13 – b + 1) – (13 – c + 1) =
52 – 14 + a – 14 + b – 14 + c =
52 – 14 – 14 – 14 + a + b + c =
10 + a + b + c
Antallet af kort i første bunke
Antallet af kort i anden bunke
Antallet af kort i tredje bunke
I bunken med de resterende kort er der altså 10 + a + b + c, så hvis vi fjerner eller tæller 10 + a + b fra, så er der c tilbage, som netop er tallet på det øverste kort i den tredje bunke af kort, som vi ikke kender. På den måde kan vi tælles os frem til det rigtige tal på det hemmelige kort.
Har du lyst til mere matematisk magi?
Hvis du har lyst til mere matematisk magi, så er der hjælp at hente på internettet. Her kan du søge dig frem til flere matematiske korttricks. Her følger nogle enkelte links, som kan føre til meget mere matematisk magi:
Stand-up Maths: Quick Mathematical Card Trick
https://www.youtube.com/watch?v=ggH8cKcPOHI
Numberphile: Beautiful Card Trick – Number 27
https://www.youtube.com/watch?v=l7lP9y7Bb5g
A Million Card Tricks: Amazing Telling Time Easy Card Trick: Version #1 (Self-Working!) https://www.youtube.com/watch?v=dmCH12wqvsk
1
3
5
7
9
2
4
6
8
10

Start debatten med en kommentar