Mon ikke de fleste vil svare Pythagoras’ læresætning på spørgsmålet om hvilken ligning, man fra matematikundervisningen husker bedst. Den daværende statsminister Helle Thorning-Schmidt henviste i sin åbningstale til Folketinget i 2012 til Pythagoræiske Læresætning, da hun fremlagde regeringens fremtidsvision for folkeskolen. Ifølge Statsministeren ville matematikken flytte til skolens værksted, og lugten af træ, lyden af saven, den rette vinkel på fuglehusets tag ville få Pythagoras’ sætning til at hænge bedre fast. Da Helle Thorning-Schmidt efterfølgende blev spurgt til, hvordan det nu lige er, Pythagoras’ læresætning lyder, kan hun ikke huske den. En par dage efter kan Statsministeren godt huske sætningen, og hun gengiver den ganske korrekt som a2 + b2 = c2. Statsministeren blev ikke spurgt om, hvad den ligning betyder. Og det var måske meget godt for Statsministeren eller journalisten, der stillede spørgsmålet. Mange kan sikkert godt huske en ligning, men hvad det er for en information den giver os er måske ikke altid helt klart. Og hvis vi ikke ved, hvad ligningen fortæller os, så den styrke ved matematiseringen af vores omgivelser, som omtales i lederen til denne udgave af MatOnline, tabt. Det kan der være mange grunde til, herunder at man ikke er bevidst om, hvad ligningen kan anvendes til. På den måde havde Helle Thorning-Schmidt jo en pointe, da hun ville flytte Pythagoras til skolens værksted. Pythagoras’ læresætning fortæller os, hvordan siderne i en trekant er relateret: Summen af katedrenes kvadrat er lig med kvadratet på hypotenusen. Altså hvis man måler siderne i en retvinklet trekant, og sætter de længder i anden, så vil summen af de mindste længder i anden være lig med den største længde i anden. Og omvendt vil en trekant, hvor siderne opfylder Pythagoras’ læresætning være en retvinklet trekant.
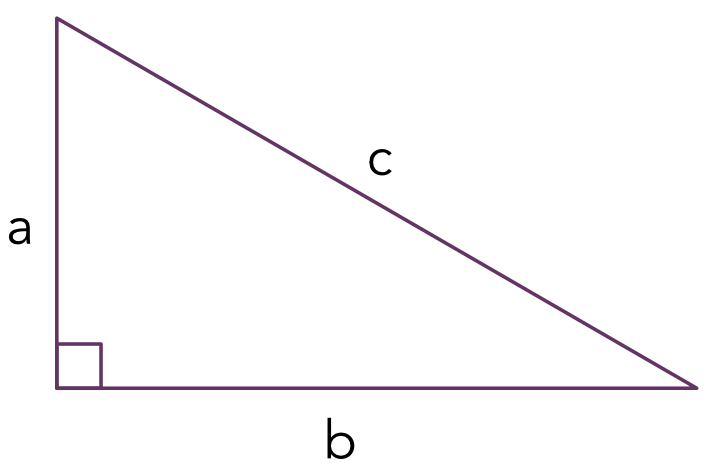
Phytagoras læresætning har stor betydning for vores beskrivelse og forståelse af rummet omkring os. Den er et uvurderligt redskab for tømreren, arkitekten, ingeniøren og navigatøren. Den forbinder geometrien med algebra ved at beskrive et geometrisk objekt, den retvinklede trekant, ved hjælp af et algebraisk udtryk, a2 + b2 = c2. Og den kan hjælpe os med at bestemme afstande og lave opmålinger. I 1615 beskrev den hollandske matematiker Willebrord Snellius (1580-1626) en metode, kaldet triangulering, til at opmåle et område. Triangulering betyder opdeling i trekanter. Det var i gamle dage det vigtigste hjælpemiddel, når man skulle lave landkort. Området, der skal opmåles, dækkes af et net af trekanter. Ideen er, at hvis man kender længde af en side af en trekant og samtidig to vinkler i samme trekant, så kan man regne de to andre sider og den sidste vinkel ud. Man vælger to punkter beliggende bekvemt i terrænet og måler så afstanden med så stor nøjagtighed som muligt, og så har med den kendte side. Så vælger man endnu et punkt, og har nu en trekant, hvor man kan måle to vinkler ved at sigte fra de to oprindelige punkter til det sidst valgte punkt. Så kender man en side og to vinkler i trekanten og kan derfor kan man regne ud, hvor lange de to øvrige sider er. Ved at fortsætte sådan kan man udregne alle siderne på alle trekanterne, der dækker området og til slut regne de afstande ud, som man ønsker at bestemme.
Phytagoras læresætning havde også afgørende betydning for opdagelsen af koordinatsystemet, der består af et system af linjer, kaldet akser, forsynet med tal. Det kendteste koordinatsystem er det såkaldte cartesiske, der besår af to akser, ofte kaldet x- og y-aksen eller første- og andenaksen, der står vinkelret på hinanden. Det blev introduceret af den franske matematiker og filosof René Descartes (1596-1650). Ved hjælp koordinatsystemet vi lave landkort, hvor en position angives ved hjælp af to tal, kaldet koordinater, ligesom vi kan repræsentere geometriske figurer ved hjælp koordinater. De to koordinattal betegnes (x,y) og giver faktisk en fuldstændig præcis placering af et punkt i koordinatsystemet.
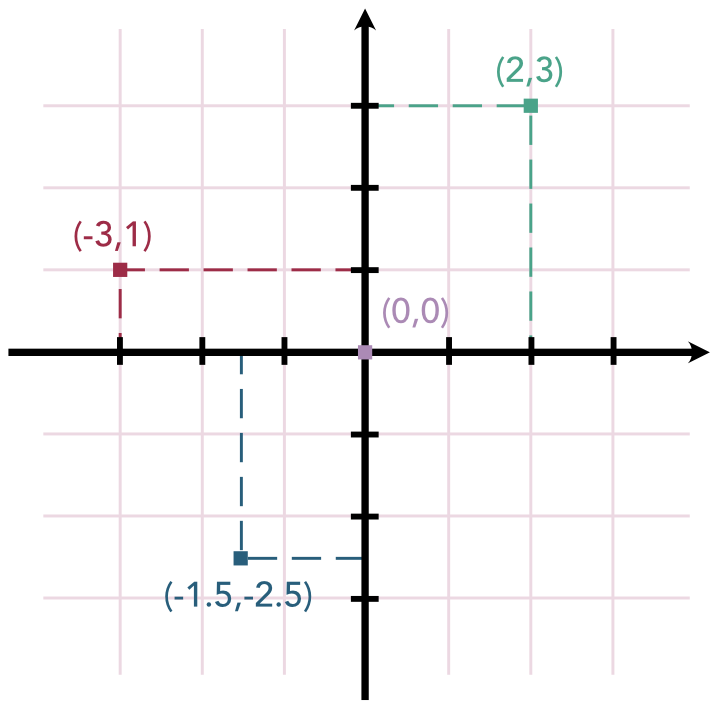
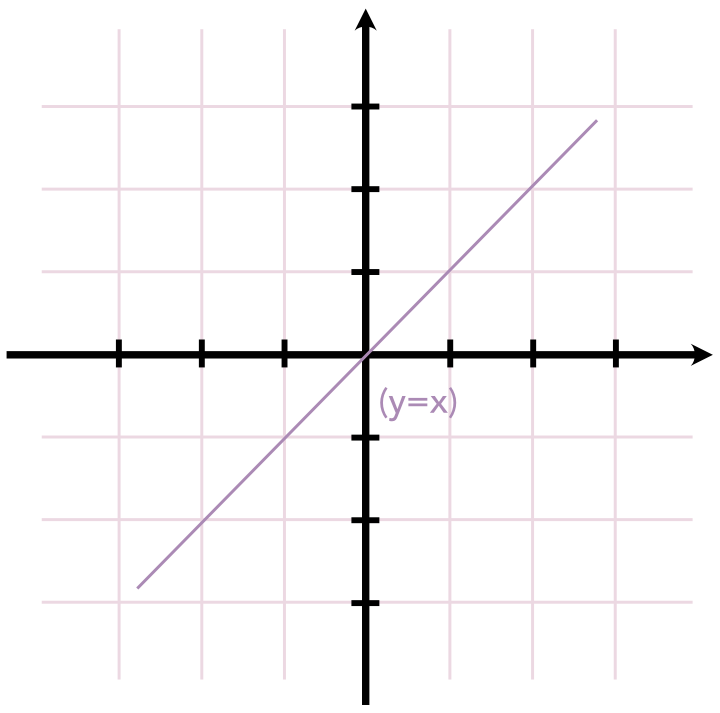
Nogen af de største europæiske matematikere i det 17. århundrede indså, at en plan linje eller kurve korresponderer til løsninger af en ligning med to ubekendte x og y. Fx vil linjen, der går gennem skæringen mellem koordinatsystemets akser og danner en vinkel med x-aksen på 45 grader svarer til ligningen y = x, fordi (x,y) ligger på den linje hvis og kun hvis y = x.
Så kan man jo spørge, hvilken ligning svarer til den geometriske figur en cirkel? Her kommer Phytagoras læresætning ind i billedet. Den fortæller nemlig, at afstanden, kaldet r, fra skæringen mellem koordinatsystemets akser til et punkt (x,y) opfylder, at x2 + y2 = r2 . Men da alle punkter med samme afstand r fra skæringen mellem koordinatsystemets akser udgør en cirkel med radius r, har vi nu cirklens ligning: x2 + y2 = r2.
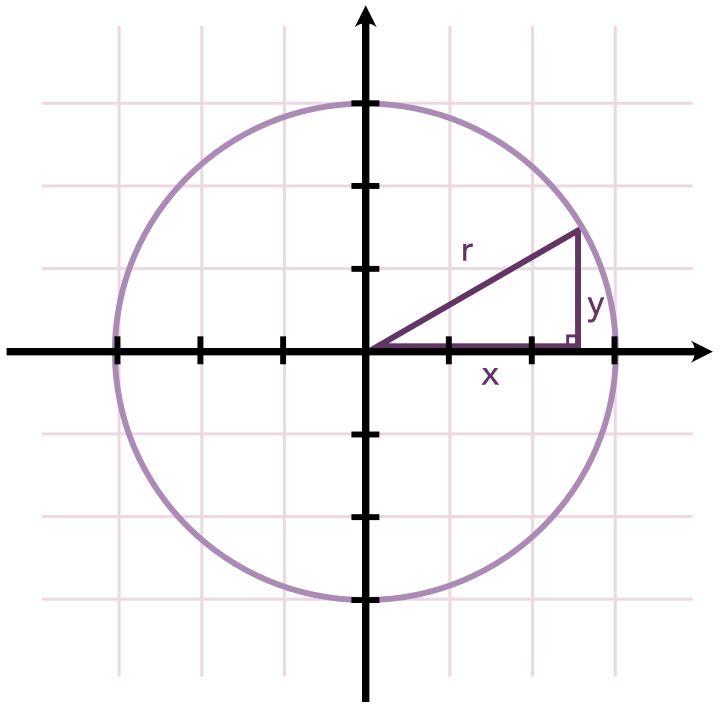

Start debatten med en kommentar