Wenn man fragt, welche Gleichung aus dem Mathematikunterricht am besten im Gedächtnis geblieben ist, werden wahrscheinlich die meisten den Satz des Pythagoras nennen. Die frühere Ministerpräsidentin Helle Thorning-Schmidt hat 2012 in ihrer Eröffnungsrede vor dem dänischen Parlament auf den Satz des Pythagoras verwiesen, als sie erläuterte, wie die Zukunftsvision der Regierung für die Volksschule aussah. Den Worten der Ministerpräsidentin zufolge sollte die Mathematik in die Werkstätten der Schulen Einzug halten, wo der Geruch nach Holz, der Klang der Säge und der rechte Winkel am Dach des Vogelhäuschens dafür sorgen würden, dass der Satz des Pythagoras besser im Gedächtnis bleibt. Als Helle Thorning-Schmidt später gefragt wurde, wie denn der Satz des Pythagoras nun eigentlich laute, konnte sie sich nicht mehr daran erinnern. Ein paar Tage später war er ihr wieder eingefallen und sie konnte ihn ganz korrekt aufsagen: a2 + b2 = c2. Was diese Gleichung bedeutet, wurde die Ministerpräsidentin nicht gefragt. Und das war vielleicht auch ganz gut für sie oder für den Journalisten, der die Frage hätte stellen können. Viele können sich vermutlich gut an die Gleichung erinnern, aber welche Information tatsächlich darin steckt, ist vielleicht nicht immer ganz so klar. Wenn wir jedoch nicht wissen, was uns die Gleichung sagt, ist die Kraft, die in der Mathematisierung unserer Umgebung liegt und die in der Einleitung zu dieser Ausgabe von MatOnline angesprochen wurde, ganz einfach verloren. Für dieses Problem kann es viele Gründe geben. So ist den Menschen möglicherweise gar nicht bewusst, wofür man die Gleichung anwenden kann. Insofern hatte Helle Thorning-Schmidt ja recht, als sie Pythagoras in den Schulwerkstätten eine neue Heimat geben wollte. Der Satz des Pythagoras verrät uns, in welchem Bezug die Seiten eines Dreiecks zueinander stehen: Die Summe der Kathetenquadrate entspricht dem Hypothenusenquadrat. Wenn man also die Seiten eines rechtwinkligen Dreiecks ausmisst und ihre Längen quadriert, dann ist die Summe der quadrierten Längen der zwei kürzeren Seiten genauso groß wie die quadrierte Länge der längsten Seite. Und umgekehrt ist ein Rechteck, dessen Seiten dem Satz des Pythagoras entsprechen, immer ein rechtwinkliges Dreieck.
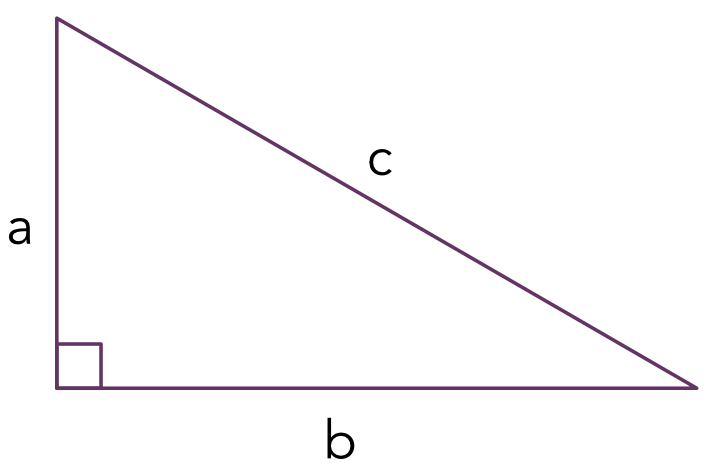
Der Satz des Pythagoras ist ausgesprochen wichtig für unsere Fähigkeit, den uns umgebenden Raum zu beschreiben und zu erfassen. Er ist ein unschätzbares Hilfsmittel für Zimmerleute, Architekten, Ingenieure und Navigatoren. Er verbindet die Geometrie mit Algebra, indem er ein geometrisches Objekt, nämlich das rechtwinklige Dreieck, mit Hilfe einer algebraischen Formel beschreibt: a2 + b2 = c2. Und er kann uns helfen, Abstände zu bestimmen und Messungen durchzuführen. Im Jahre 1615 beschrieb der niederländische Mathematiker Willebrord Snellius (1580-1626) eine Methode zur Bemessung von Flächen, die als „Triangulation“ bezeichnet wird. Der Begriff steht für eine Aufteilung in Dreiecke. Das Verfahren war damals das wichtigste Hilfsmittel beim Anfertigen von Landkarten. Die Fläche, die ausgemessen werden sollte, wurde mit einem Netz aus Dreiecken bedeckt. Die Idee dahinter ist Folgende: Wenn man bei einem Dreieck die Länge einer Seite und zwei Winkel kennt, kann man die anderen zwei Seiten und den letzten Winkel berechnen. Man sucht sich zwei Punkte aus, die bequem im Gelände liegen, und misst den Abstand zwischen ihnen so genau wie möglich aus. Damit hat man die bekannte Seite. Dann sucht man sich einen weiteren Punkt und hat nun ein Dreieck, in dem man zwei Winkel messen kann, indem man von den zwei ursprünglichen Punkten auf den zuletzt ausgesuchten Punkt blickt. Jetzt kennt man eine Seite und zwei Winkel des Dreiecks und kann sich dementsprechend ausrechnen, wie lang die beiden verbleibenden Seiten sind. Wenn man dieses Vorgehen fortsetzt, kann man alle Seiten aller Dreiecke berechnen, die über der Fläche liegen, und zum Schluss die Abstände ermitteln, die man bestimmen möchte.
Der Satz des Pythagoras war auch entscheidend für die Entdeckung des Koordinatensystems, das aus einem System aus Linien („Achsen“ genannt) besteht, die mit Zahlen versehen werden. Das bekannteste Koordinatensystem ist dabei das so genannte „kartesische Koordinatensystem“, das aus zwei Achsen besteht. Die beiden Achsen sind rechtwinklig zueinander angeordnet und werden oftmals als x- und y-Achse oder als erste und zweite Achse bezeichnet. Eingeführt wurde es von dem französischen Mathematiker und Philosophen René Descartes (1596-1650). Mit der Hilfe des Koordinatensystems erstellen wir Landkarten, in denen wir mit zwei Zahlen, den „Koordinaten“, Positionen angeben können. Auch geometrische Figuren können mit Koordinaten dargestellt werden. Die beiden Koordinatenzahlen, die man als (x, y) wiedergibt, sind eine absolut präzise Benennung eines bestimmten, innerhalb des Koordinatensystems liegenden Punktes.
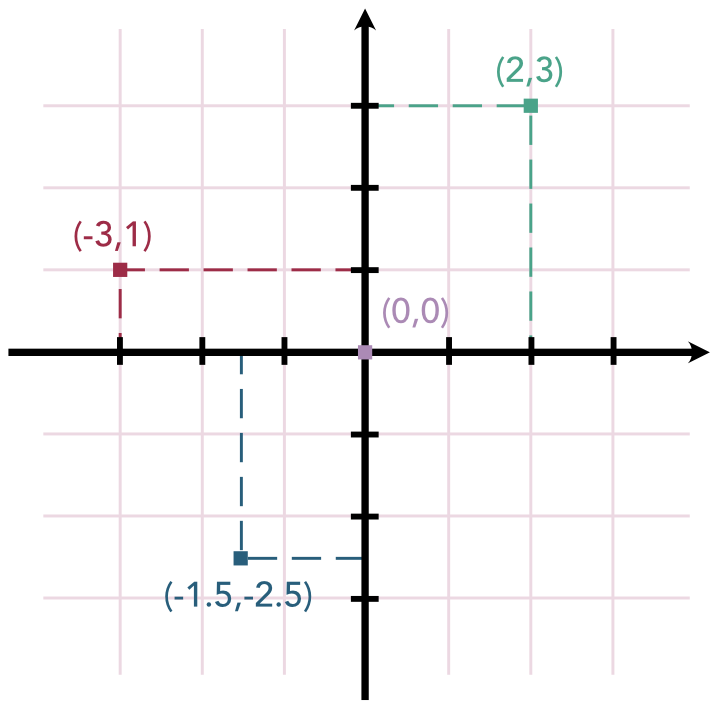
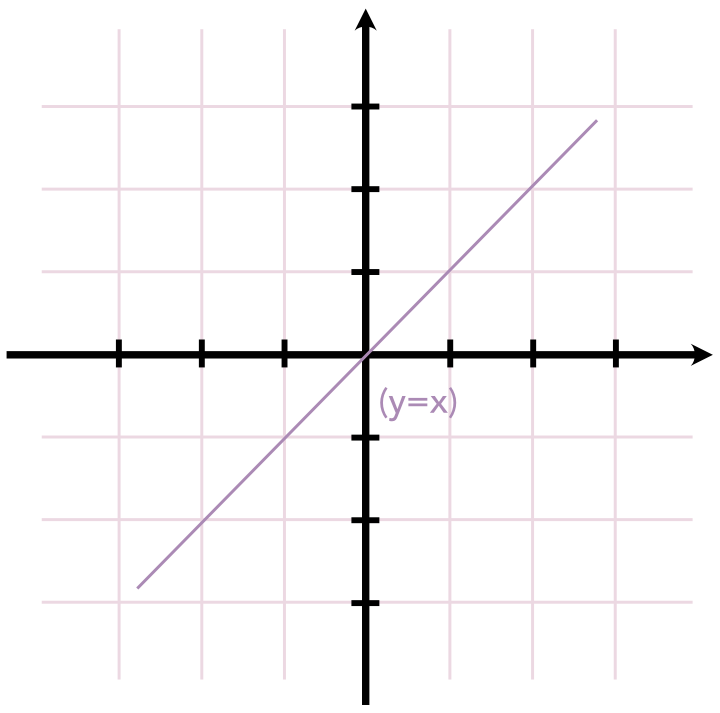
Einige der größten europäischen Mathematiker des 17 Jahrhunderts kamen zu der Erkenntnis, dass es zwischen einer geraden Linie oder Kurve und der Lösung einer Gleichung mit den zwei Unbekannten x und y einen Zusammenhang gibt. So entspricht beispielsweise die Linie, die durch den Schnittpunkt der Achsen des Koordinatensystems verläuft und einen 45-Grad-Winkel mit der x-Achse bildet, der Gleichung y = x, da (x, y) auf dieser Linie liegen, wenn – und nur wenn – y = x ist.
Nun könnte man sich die Frage stellen, welche Gleichung denn der geometrischen Figur des Kreises entspricht? Hier kommt der Satz des Pythagoras ins Spiel. Er verrät uns nämlich, dass der „r“ genannte Abstand zwischen dem Schnittpunkt der Koordinatenachsen und dem Punkt (x, y) der Gleichung x2 + y2 = r2 entspricht. Da aber alle Punkte, bei denen der Abstand r vom Schnittpunkt der Koordinatenachsen aus gesehen gleich ist, einen Kreis mit dem Radius r bilden, haben wir auf diese Weise die Gleichung für einen Kreis gefunden: x2 + y2 = r2.
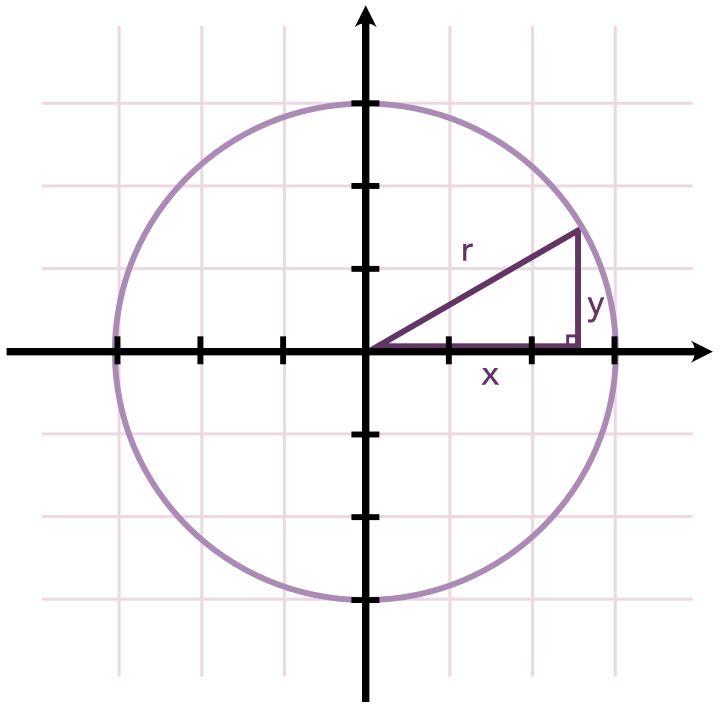

Gib den ersten Kommentar ab