Die Normalverteilung, die um das Jahr 1730 herum vom Mathematiker Abraham de Moivre (1667-1754) eingeführt wurde, ist eines der bekanntesten naturwissenschaftlichen Modelle überhaupt. Sie beschreibt die theoretisch ideale Verteilung einer Reihe von Beobachtungswerten und wird verwendet, um zu beschreiben, wie sich eine große Menge an Beobachtungen, wie beispielsweise die Größe oder das Gewicht jeder einzelnen Person einer großen und homogenen Gruppe, rund um den Durchschnittswert (Mittelwert) herum verteilt (Streuung). Hat man beispielsweise die Größe von 1.000 Menschen ausgemessen und sieht sich an, wie ihre Größenverteilung aussieht, wird man oftmals feststellen, dass der Großteil der gemessenen Werte rund um einen Durchschnittswert herum angeordnet ist. Je weiter man sich von diesem Durchschnitt entfernt, desto mehr nimmt die Anzahl der in diesem Bereich liegenden Beobachtungswerte ab. So macht die Normalverteilung ihrem Namen wirklich alle Ehre, denn sie zeigt eine Verteilung der Messergebnisse, die in vielen Situationen auf ganz natürliche Weise auftritt, wenn man ein bestimmtes Phänomen beschreiben möchte. Das kann beispielsweise die Wahrscheinlichkeit sein, bei zahlreichen Münzwürfen eine bestimmte Anzahl von Malen „Kopf“ zu werfen. Bei 100 Würfen ist es am wahrscheinlichsten, 50 Mal Kopf zu werfen, aber alles zwischen 40 und 60 ist auch nicht unwahrscheinlich, während 0 Mal nahezu undenkbar ist. Das Modell wird grafisch oftmals mit Hilfe der Glockenkurve oder „Bell Curve“ dargestellt, wobei der Höhepunkt der Kurve den Mittelwert des statistischen Materials wiedergibt und ihre Breite ein Maß dafür ist, wie sich die Beobachtungen verteilen. Letzteres wird auch als Streuung oder Standardabweichung bezeichnet.
Unsere heutige Wahrscheinlichkeitsrechnung und Statistik fußt auf der Normalverteilung, die damit in unzähligen Zusammenhängen zum Einsatz kommt. Wie beispielsweise bei der Mobiltelefonie und der Übertragung von Fernseh- und Radioprogrammen, wenn man die atmosphärischen Störungen ausgleichen möchte, die sich auf die Signale der drahtlosen Kommunikation auswirken. Die Summe dieser zufällig und natürlich vorkommenden Signalstörungen ist normalverteilt. Die Normalverteilung wird auch in der Pharmaindustrie verwendet, wenn es um die Dokumentation eines neuen Medikaments geht. Hier möchte man üblicherweise die Unsicherheiten berechnen, die es in Bezug auf die durchschnittliche Wirkung des Medikaments gibt, was oftmals Berechnungen der Normalverteilung beinhaltet.
Der Einsatz der Normalverteilung ist weit verbreitet, aber in manchen Fällen nicht unumstritten. So brachten zwei Amerikaner, der Psychologe Richard J. Hernstein und der Politologe Charles Murray, im Jahre 1964 das Buch „The Bell Curve“ heraus. Eine der Hauptthesen dieses Buches besagte, dass es einen Zusammenhang zwischen der mit Hilfe des Intelligenzquotienten (IQ) bemessenen Intelligenz und sozialen Variablen gäbe, wie dem Einkommen, der Beschäftigung und Kriminalität. Darauf aufbauend argumentieren die Verfasser, dass der IQ eines Menschen besser geeignet sei, um soziale Variablen vorherzusagen, als der soziale und wirtschaftliche Hintergrund der Eltern und das Bildungsniveau. Das Buch löste unter anderem eine Diskussion darüber aus, inwieweit Unterschiede im IQ einen genetischen Ursprung haben, was zu dem Vorschlag führte, die Einwanderung und das Recht armer Frauen auf Fortpflanzung zu beschränken.
Leider hat es im Laufe der Geschichte viele Beispiele dafür gegeben, wie die Mathematik missbraucht werden kann, um ethnische und soziale Vorurteile zu stützen, wie beispielsweise in Verbindung mit dem Geschlecht, der Rasse, den Genen und dem Rassismus. Aus diesem Grunde ist es wichtig, beim Einsatz von mathematischen Graphen nicht unkritisch zu sein. Ebenso wichtig ist es aber auch, dass wir in der Lage sind, aus einem Graphen die oftmals umfassenden wissenschaftlichen Informationen herauszufiltern, die dieser enthält, und die Ergebnisse konstruktiv anzuwenden. Wie der bekannte deutsche Soziologe Ulrich Beck in seinem Hauptwerk „Risikogesellschaft“ angemerkt hat, ist eine wissenschaftliche Rationalität ohne gesellschaftliche Rationalität ebenso leer wie eine gesellschaftliche Rationalität ohne wissenschaftliche Rationalität. Insofern gibt es das Paradoxon, dass die Mathematik danach strebt, für allgemeine Phänomene und Prozesse in der Natur und der Gesellschaft eine objektive Erklärung zu geben, während sie gleichzeitig sehr wertbeladen sein kann, wenn ein gesellschaftlicher Plan ins Spiel kommt.
Sehen wir uns einmal an, welche Relevanz die Deutung von Graphen für unsere Auffassung von menschlicher Vielfalt und Homogenität und unser Verständnis dieser Punkte haben kann. Unten sehen wir Normalverteilungskurven für zwei menschliche Populationen. Was die Kurven über die zwei Populationen aussagen, ist für uns gar nicht wichtig, aber es könnte sich beispielsweise um die Verteilung von Behinderungen bei Europäern und Afrikanern handeln.
Unsere heutige Wahrscheinlichkeitsrechnung und Statistik fußt auf der Normalverteilung, die damit in unzähligen Zusammenhängen zum Einsatz kommt. Wie beispielsweise bei der Mobiltelefonie und der Übertragung von Fernseh- und Radioprogrammen, wenn man die atmosphärischen Störungen ausgleichen möchte, die sich auf die Signale der drahtlosen Kommunikation auswirken. Die Summe dieser zufällig und natürlich vorkommenden Signalstörungen ist normalverteilt. Die Normalverteilung wird auch in der Pharmaindustrie verwendet, wenn es um die Dokumentation eines neuen Medikaments geht. Hier möchte man üblicherweise die Unsicherheiten berechnen, die es in Bezug auf die durchschnittliche Wirkung des Medikaments gibt, was oftmals Berechnungen der Normalverteilung beinhaltet.
Der Einsatz der Normalverteilung ist weit verbreitet, aber in manchen Fällen nicht unumstritten. So brachten zwei Amerikaner, der Psychologe Richard J. Hernstein und der Politologe Charles Murray, im Jahre 1964 das Buch „The Bell Curve“ heraus. Eine der Hauptthesen dieses Buches besagte, dass es einen Zusammenhang zwischen der mit Hilfe des Intelligenzquotienten (IQ) bemessenen Intelligenz und sozialen Variablen gäbe, wie dem Einkommen, der Beschäftigung und Kriminalität. Darauf aufbauend argumentieren die Verfasser, dass der IQ eines Menschen besser geeignet sei, um soziale Variablen vorherzusagen, als der soziale und wirtschaftliche Hintergrund der Eltern und das Bildungsniveau. Das Buch löste unter anderem eine Diskussion darüber aus, inwieweit Unterschiede im IQ einen genetischen Ursprung haben, was zu dem Vorschlag führte, die Einwanderung und das Recht armer Frauen auf Fortpflanzung zu beschränken.
Leider hat es im Laufe der Geschichte viele Beispiele dafür gegeben, wie die Mathematik missbraucht werden kann, um ethnische und soziale Vorurteile zu stützen, wie beispielsweise in Verbindung mit dem Geschlecht, der Rasse, den Genen und dem Rassismus. Aus diesem Grunde ist es wichtig, beim Einsatz von mathematischen Graphen nicht unkritisch zu sein. Ebenso wichtig ist es aber auch, dass wir in der Lage sind, aus einem Graphen die oftmals umfassenden wissenschaftlichen Informationen herauszufiltern, die dieser enthält, und die Ergebnisse konstruktiv anzuwenden. Wie der bekannte deutsche Soziologe Ulrich Beck in seinem Hauptwerk „Risikogesellschaft“ angemerkt hat, ist eine wissenschaftliche Rationalität ohne gesellschaftliche Rationalität ebenso leer wie eine gesellschaftliche Rationalität ohne wissenschaftliche Rationalität. Insofern gibt es das Paradoxon, dass die Mathematik danach strebt, für allgemeine Phänomene und Prozesse in der Natur und der Gesellschaft eine objektive Erklärung zu geben, während sie gleichzeitig sehr wertbeladen sein kann, wenn ein gesellschaftlicher Plan ins Spiel kommt.
Sehen wir uns einmal an, welche Relevanz die Deutung von Graphen für unsere Auffassung von menschlicher Vielfalt und Homogenität und unser Verständnis dieser Punkte haben kann. Unten sehen wir Normalverteilungskurven für zwei menschliche Populationen. Was die Kurven über die zwei Populationen aussagen, ist für uns gar nicht wichtig, aber es könnte sich beispielsweise um die Verteilung von Behinderungen bei Europäern und Afrikanern handeln.
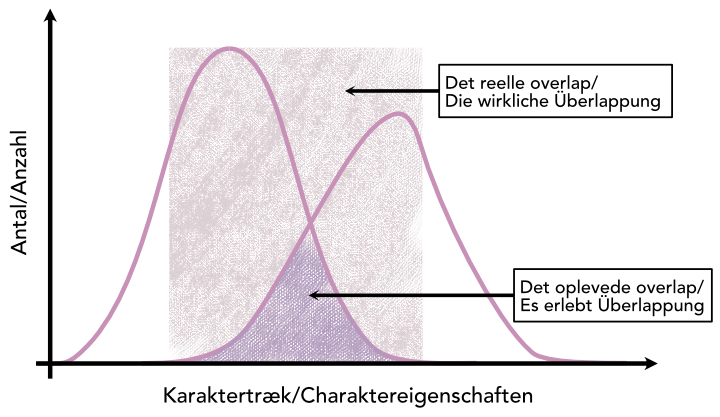
Eine Deutung, die sich hier quasi auf den ersten Blick aufdrängt, wäre die, dass der dreieckige Bereich zwischen den beiden Kurven das darstellt, was die beiden Populationen eint. Diese Deutungsweise unterstreicht die Unterschiede zwischen den Populationen und führt zu der Auffassung, dass die beiden Populationen nur sehr wenig gemeinsam haben. Der wirkliche Overlap bei den beiden Populationen ist jedoch der Bereich, in dem die beiden Kurven auf der ersten Achse die gleichen Werte haben. Dieser Bereich ist erheblich größer als der dreieckige Bereich und beinhaltet den Median beider Populationen, wie man bei einem geordneten Satz an Beobachtungen den Mittelwert bezeichnet. Die Medianwerte beinhalten somit keine Informationen über Individuen in den beiden Populationen, wie beispielsweise zu deren Rasse oder anderen Arten der Unterteilung. Ein Graph kann also nicht ohne kritische Analyse eingesetzt werden, und zwar sowohl im Hinblick auf seine Brauchbarkeit und Relevanz als auch im Hinblick auf den Vergleich mit anderen Graphen und deren Ergebnissen.

Gib den ersten Kommentar ab