MatKult-Mathematikwoche

Für die Woche der Mathematik Ende Mai, wurden fünf Postkarten mit mathematischen ‚Kopfzerbrechern‘ hergestellt. Im Folgenden können Sie mehr über die Postkarten und ihren Inhalt lesen.

Krieche durch die Karte – kann das Loch in einem Gegenstand größer sein als der Gegenstand selbst?

Aus dem Stehgreif die klare Antwort: Nein; geht ja gar nicht! — Geht aber doch!

Ein kleines Loch in einer zweidimensionalen flachen Postkarte kann vergrößert werden, indem man hineinschneidet und die Karte dreidimensional biegt und wölbt — und so kann man selbst durch eine Postkarte kriechen.

Eine ebenso überraschende Tatsache (für diejenigen, die es noch nicht wissen) ist, dass eine dänische 5-Kronenmünze durch ein Loch in einem Stück Papier von der Größe der kleineren dänischen 2-Kronenmünze passt. Oder, um es etwas mathematischer zu formulieren: Eine Münze passt durch ein Loch in einem Papierbogen, dessen (das Loch!) Durchmesser kleiner ist als der der Münze selbst.

Praxisversuch: Nehmen Sie ein normales Stück Papier, ziehen Sie darauf den Umriss einer dänischen 1-Kronemünze nach und schneiden Sie entlang dieser Umrisslinie ein Loch. Das Loch im Papier wird natürlich etwas größer als eine 1-Kronemünze sein, aber sein Durchmesser ist dennoch kleiner als der der anderen dänischen Kronenmünzen. Trotzdem passen alle größeren Münzen durch das Loch, ohne dass das Papier weiter eingeschnitten werden muss! N-na!, denken Sie … wie soll das denn gehen?!

Doch-doch, es stimmt. Wenn Sie das Loch in der Mitte falten und vorsichtig an den „Enden“ des Lochs ziehen, verdreht sich das Papier, und mit ein wenig vorsichtigem Ziehen und Zupfen passt sogar die große 5-Kronen-Münze durch das Loch hindurch. Statt eines kreisrunden Lochs erhält man ein längliches, schmales Loch, durch das die Münzen durchrutschen können. Überzeugen Sie sich selbst!

Kann man das auch mit einem 10-Cent-Stück machen und die anderen Euro-Münzen durch das Loch hindurchschieben?

Wenn man das Loch im Papier ganz herauszieht, könnte man theoretisch eine Länge erhalten, die halb so groß ist wie der Lochumfang. Vergleichen wir dies mit dem Verhältnis zwischen Umfang und Durchmesser eines Kreises: Umfang = π Durchmesser, so ergibt sich — theoretisch —, dass wir eine vollkommen flache Münze mit einem Durchmesser π/2≈1,57 Mal größer als der Lochdurchmesser durch das Loch hindurch’wurschteln‘ könnten. In der Praxis wird es jedoch aufgrund der Steifigkeit des Papiers schwierig sein, dieses theoretische Maximum zu erreichen.

Etwas ähnliches ist auch mit nicht-flachen Gegenständen möglich. Hier mehr dazu: Stand-up Maths – Can you make a hole in a thing bigger than the thing?: https://www.youtube.com/watch?v=gPIRLQZnRNk

Das Vierfarbenproblem

Wenn man sich besonders alte Atlanten ansieht, sind die verschiedenen Länder unterschiedlich eingefärbt — und zwar so, dass zwei Länder, die eine gemeinsame Grenze haben, nicht die gleiche Farbe haben. Im Jahr 1852 entdeckte der Mathematiker Francis Guthrie, dass er die englischen Grafschaften auf diese Weise einfärben konnte, allerdings mit nur vier verschiedenen Farben. So fragte er sich, ob vier Farben immer ausreichen, um Flächen auf einer Karte einzufärben. Es sollten indessen noch über hundert Jahre vergehen, bis diese seine Frage endgültig beantwortet war. Denn erst 1970 wurde mathematisch bewiesen, dass vier Farben immer ausreichen werden. Erwähnenswert ist, dass dies der erste mathematische Satz ist, der mit Hilfe eines Computers bewiesen wurde.

Numberphile mit Professor James Grimes: https://www.youtube.com/watch?v=NgbK43jB4rQ

Monty Hall

Manchmal werden wir von unserer mathematischen Intuition getäuscht. Besonders bei Wahrscheinlichkeiten kann dies eine Herausforderung sein. Ein klassisches Beispiel hierfür stammt aus einer amerikanischen Quizsendung, deren Moderator Monty Hall hieß, weshalb das Problem auch Monty-Hall-Problem genannt wird. Lesen und sehen Sie mehr unter diesen beiden Links:

Dänisch: https://da.wikipedia.org/wiki/Monty_Hall-problemet

Deutsch: https://de.wikipedia.org/wiki/Ziegenproblem

Numberphile mit Lisa Goldberg: https://www.youtube.com/watch?v=4Lb-6rxZxx0

Einstrichzeichnungen

Manche Strichzeichnungen lassen sich mit einem einzigen langen Strich, ohne Anheben des Stifts, zeichnen — und andere nicht. Die als Graphentheorie bezeichnete mathematische Disziplin kann Ihnen bei der Beantwortung der Frage helfen, welche Zeichnungen mit einem Strich möglich sind, und welche mehr als einen Strich erfordern. Wie das geht, erfahren Sie in diesen beiden MatOnline-Beiträgen:

Dänisch: https://www.matkult.eu/matonline/index.php/2019/matematiske-puslerier-med-streger/

Deutsch: https://www.matkult.eu/matonline/index.php/de/2019/die-mathematik-hilft-graphentheorie/

Dänisch: https://www.matkult.eu/matonline/index.php/2020/matematiske-puslerier-med-streger-ii/

Deutsch: https://www.matkult.eu/matonline/index.php/de/2020/mathematische-ratsel-mit-linien-ii/

Gibt es Mathematikaufgaben, bei denen alle Antworten richtig sind?

Viele Menschen meinen, bei Matheaufgaben könne es immer nur eine richtige Antwort geben — und dass es in der Mathematik genau darum gehe: die richtige Methode anzuwenden, um die richtige Antwort zu finden, und das möglichst schnell.

Aber so ist es nicht — jedenfalls nicht nur!

Gute und interessante Mathematikaufgaben können oft auf viele verschiedene Arten beantwortet werden, und es kann durchaus mehr als eine richtige Antwort geben.

Zurück zur Frage in der Überschrift: Gibt es Mathematikaufgaben, bei denen alle Antworten richtig sind? Ja, die gibt es! Auf MatOnline im Beitrag Welcher passt nicht dazu? ist diese Art von Aufgaben thematisiert worden. Und hier sind noch einige mehr — verbunden mit der Aufforderung, auch selbst solche Aufgaben zu konstruieren.

Dieser Aufgabentyp besteht aus vier Objekten. Dabei kann es sich um Zahlen, Figuren, Bilder oder Diagramme handeln. Nur die Phantasie setzt hier Grenzen. Die Frage ist immer die gleiche: Welche/r/s der Vier passt nicht dazu?

Hier sehen wir eine ”Welcher passt nicht dazu?”-Aufgabe, und zwar ausgehend von vier Karten des SET-Kartenspiels. Mehr über das SET-Spiel sehen Sie hier. Versuchen Sie erstmal selbst, ein paar Antworten zu geben.

Die Karte oben links sticht heraus, weil sie grün ist und die anderen drei rot sind.
Ja, schon, aber man könnte auch sagen, dass die Karte oben rechts nicht zum Rest passt, weil ihre Figuren rautenförmig, die der drei anderen aber schlangenförmig sind.
Aber die Karte unten links hat drei Figuren, alle anderen nur zwei; ergo passt SIE nicht.
Auf der letzten Karte unten sind die Figuren nicht ausgemalt; daher passt SIE nicht.

Schlussfolgerung: Alle Karten passen irgendwie nicht — jede auf ihre Weise. Also sind alle Antworten richtig. Die Hausforderung ist das Argumentieren, warum angeblich genau diese oder jene Karte aus dem Rahmen fällt.

Noch eine Aufgabe — dieses Mal mit vier ’normalen‘ Spielkarten. Vielleicht a bisserl schwieriger, aber versuchen Sie sich dennoch mit einer passenden Erklärung:

Warum passt die Pik 4 nicht zum Rest?
Warum passt die Karo 5 nicht zum Rest?
Warum passt die Dame nicht zum Rest?
Warum passt die Herz 8 nicht zum Rest?

Es könnte hier hilfreich sein, über die Eigenschaften der Zahlen und Formen auf den Karten nachzudenken.

Sie könnten auch eine*n Freund*in bitten, sich die Karten anzusehen. Ihm oder ihr fällt vielleicht etwas anderes auf — aber das ist auch gar nicht wichtig. Wichtig ist, für die eigene Sichtweise gut argumentieren zu können.

Mir fielen beim Konstruieren der Aufgabe folgende Argumente ein:

Die Pik 4 ist schwarz.
5 ist eine ungerade Zahl.
Die Dame ist die einzige Bildkarte.
Die Herz 8 ist die einzige Karte, bei der eine Drehung um 180 Grad erkennbar wäre. Die anderen sind drehsymmetrisch.

Vielleicht sind Ihnen noch andere Argumente eingefallen. Das wäre prima, denn dann gäbe es noch mehr Möglichkeiten, die Aufgabe zu lösen — UND Anlass zu guten Gesprächen über die Eigenschaften der jeweiligen Karten.

Diese Art von Aufgaben wurde von Christopher Danielson so konzipiert, dass sie unsere Neugier kitzeln und zu guten Gesprächen über mathematische Eigenschaften führen können. Er ist der Urheber des Bildbandes ”Which One Doesn’t Belong?” für Kinder — mit Figurenaufgaben nach dem Motto ”Welcher passt nicht dazu?”.

Hier zum Ende hin noch zwei weitere Aufgaben — von der Webseite https://wodb.ca/, wobei WODB für ”Which One Doesn’t Belong” steht. Auf dieser Seite gibt es eine Vielzahl solcher ”Welcher passt nicht dazu?”-Aufgaben.

Zum Beispiel eine mit vier Zahlen und eine mit unterschiedlich konzipierten Dreiecken:

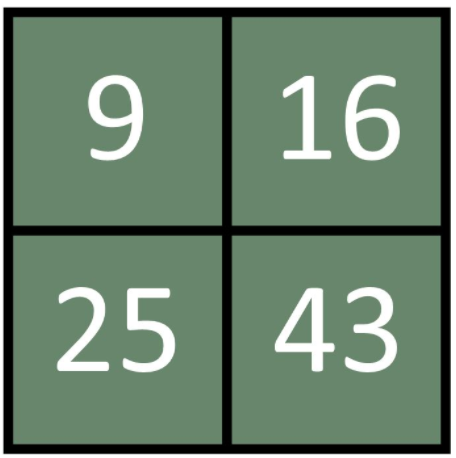
Argumentieren ließe sich dabei z. B. folgendermaßen:

Zahlenaufgabe

Die 9 hat nicht die Quersumme 7.
Die 16 ist eine gerade Zahl. Und sie ist durch 4 teilbar.
Die 25 ist die Summe aus zwei der anderen Zahlen. Und 100 ist durch sie teilbar.
Die 43 ist eine Primzahl. Und sie ist keine Quadratzahl.

Dreiecksaufgabe

Oben links: die einzige Figur, die aus verschiedenen inneren Figuren besteht. Die einzige, bei der die inneren Figuren nicht kongruent sind. Die einzige, die nicht drehsymmetrisch ist.
Oben rechts: Die einzige Figur mit vier inneren Figuren. Die einzige, bei der die inneren Figuren die gleiche Form haben wie die Figur selbst. Die einzige, bei der alle Winkel gleich sind (60 Grad).
Unten links: die einzige Figur, die rechte Winkel enthält. Das einzige Dreieck, das auf der Spitze steht.
Unten rechts: die einzige Figur, die konkave Innenfiguren hat. Die einzige mit Winkeln größer als 180 Grad. Die einzige Figur, die nicht spiegelsymmetrisch ist.

Versuchen Sie selbst, ein paar WODB-Aufgaben zu konstruieren.

Dieser Aufgabentyp ist auch in diesem MatOnline-Artikel beschrieben:

Dänisch: https://www.matkult.eu/matonline/index.php/2022/hvilken-hoerer-ikke-til/

Deutsch: https://www.matkult.eu/matonline/index.php/de/2022/hvilken-hoerer-ikke-til-2/