Hast du schon einmal darüber nachgedacht, warum ein klassischer Fußball so aussieht, wie er aussieht? Warum setzt er sich aus unterschiedlichen Formen zusammen? Ist er mathematisch gesehen eigentlich rund? Wie macht man etwas Rundes aus etwas Flachem? Könnte er auch anders aussehen? All das und vieles mehr kannst du in diesem Artikel erfahren.
Den Allermeisten wird das Fußballspiel wohl ein Begriff sein, aber solltest du davon noch nichts gehört haben, erklären wir hier kurz, worum es geht. Fußball ist ein Sport für zwei Mannschaften mit je 11 Spielern. Ganz vereinfacht gesagt spielen die Spieler mit einem speziellen Ball, wobei jede Mannschaft darum kämpft, den Ball öfter als die andere Mannschaft in das Tor des Gegners zu schießen. Jede Mannschaft hat einen Torwart, der den Ball in manchen Situationen mit den Händen berühren darf, während alle anderen Spieler nur die Füße benutzen dürfen. Um diesen Sport auszuüben, braucht man kaum anderes Zubehör als einen Fußball, was vielleicht der Grund dafür ist, dass er weltweit zu den am stärksten verbreiteten Sportarten zählt.
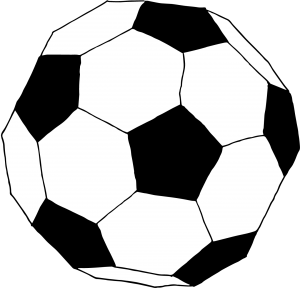
Sowohl Dänemark als auch Deutschland haben eine lange Fußballtradition. Einer der dänischen Höhepunkte war jener grandiose Moment, als Dänemark 1992 im EM-Finale in Schweden Deutschland mit 2:0 besiegte. Deutschland hingegen hat sowohl bei Europa- als auch bei Weltmeisterschaften schon öfter oben auf dem Treppchen gestanden. Ganze 3 Mal konnten die Deutschen den EM-Pokal mit nach Hause nehmen: 1972 nach einem 3:0 gegen die Sowjetunion, 1980 nach einem 2:1 gegen Belgien und 1996 nach einem 2:1 gegen Tschechien. Auch den Titel „Weltmeister“ hat sich Deutschland bereits 4 Mal auf die Visitenkarte schreiben können, und zwar 1972 nach einem 3:2 gegen Ungarn, 1980 nach einem 2:1 gegen die Niederlande sowie 1990 und 2014 nach einem 1:0-Sieg gegen Argentinien. Der klassische schwarz-weiße Fußball, um den es in diesem Artikel geht, ist dabei über Jahrzehnte hinweg in den Finalspielen über den Platz gerollt. Sein erster Einsatz fand während der EM des Jahres 1968 statt, und 1970 wurde er in Mexiko erstmals als offizieller Ball für eine WM verwendet.
| Faktenbox |
|---|
| Bei einer gleichseitigen Figur (2D) sind alle Kanten (Seiten) genau gleich lang und alle Winkel (Ecken) gleich. Ein Quadrat ist dementsprechend ein gutes Beispiel für eine solche gleichseitige Figur. Fünfecke nennen wir in der Mathematik „Pentagon“. Wir kennen das Wort vom amerikanischen Verteidigungsministerium, das tatsächlich nicht nur die Form eines Fünfecks hat, sondern auch noch ein gleichseitiges Fünfeck ist. Sechsecke nennen wir „Hexagon“. Gleichseitige Hexagone kennen wir von Bienenstöcken, deren Waben exakt diese Form haben. |
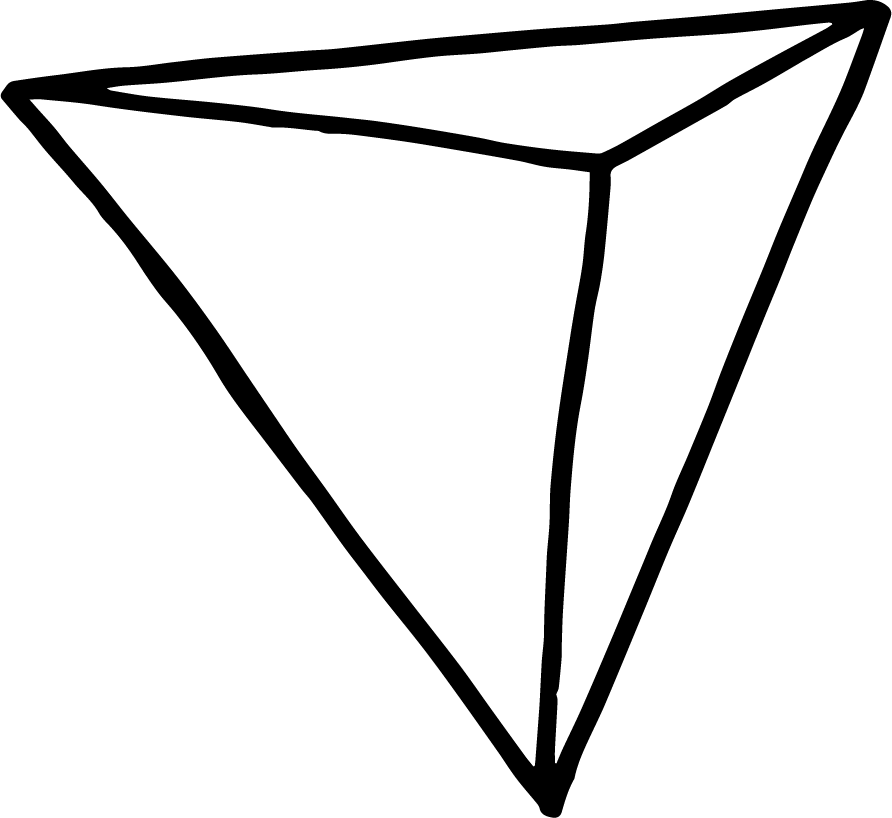
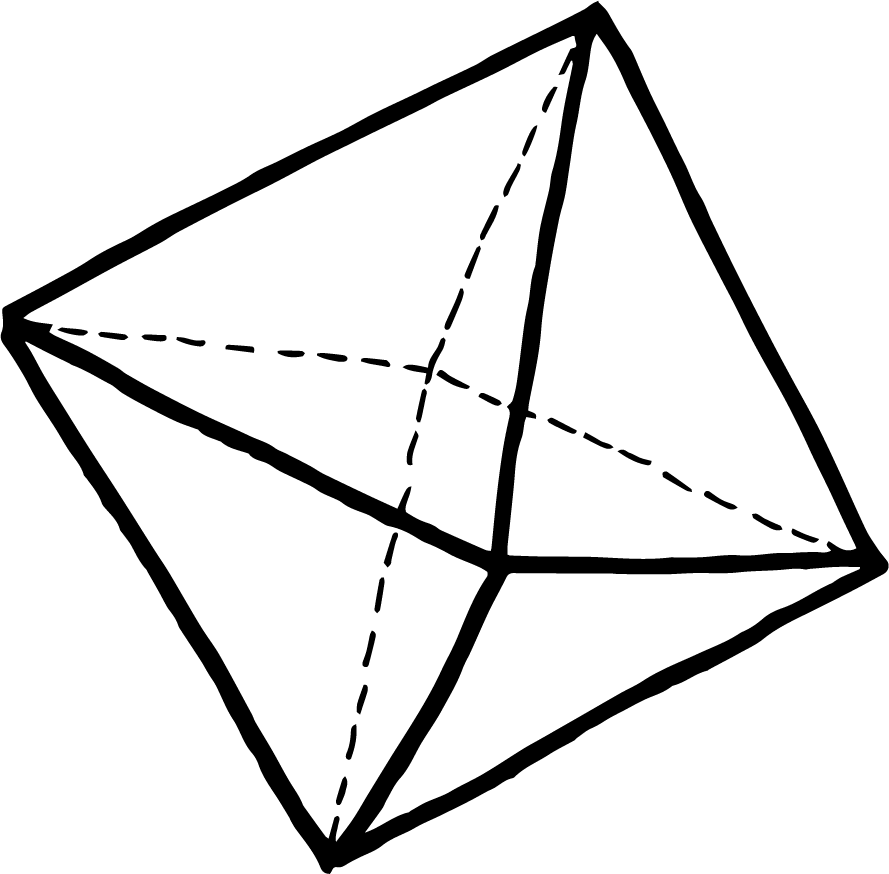

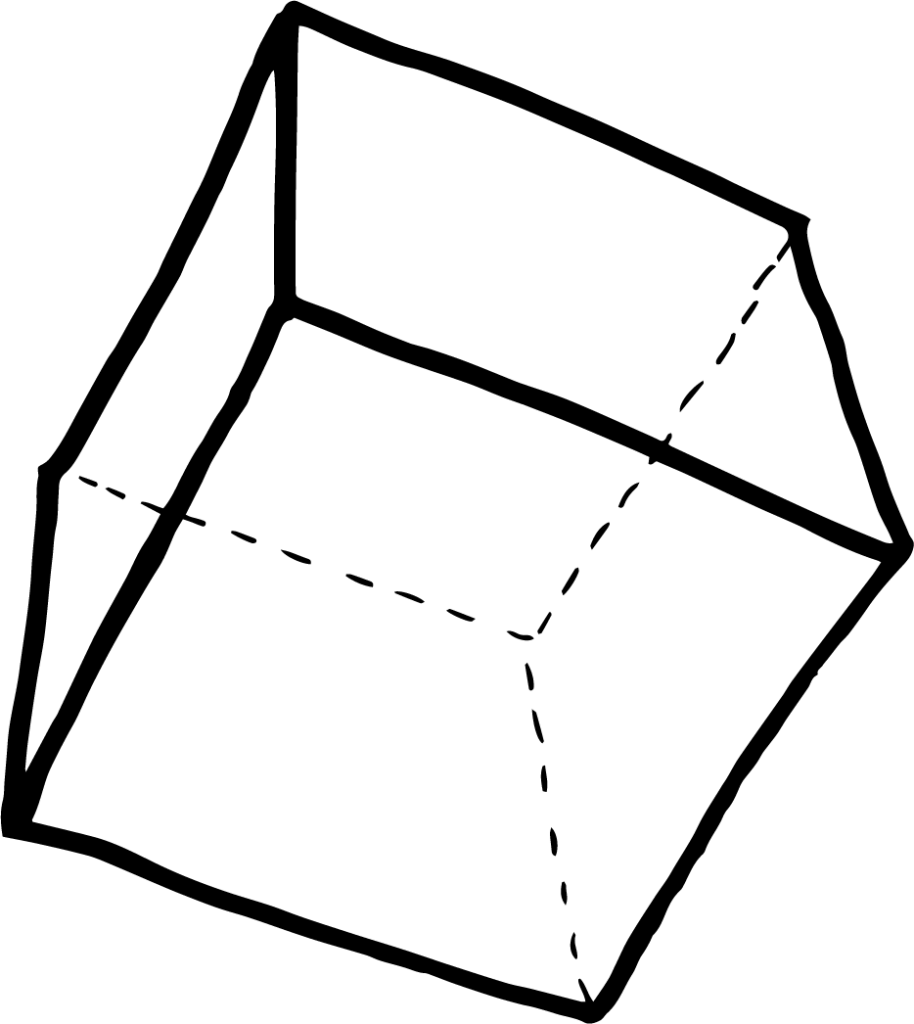

Wenn wir eine etwas rundere Form erreichen möchten, könnten wir versuchen, unseren Ball als Ikosaeder zu gestalten. So würde er aus 20 gleichseitigen Dreiecken bestehen, von denen jeweils 5 an 12 Ecken aufeinander treffen. Eine solche räumliche Figur würde, wie man auf dem Bild weiter oben gut erkennen kann, für einen runderen Ball sorgen, aber dieser Ball wäre nach wie vor ziemlich unberechenbar, da er immer noch in alle Richtungen springen und rollen könnte – je nachdem, wie er landet.
Wenn wir uns jetzt vorstellen, dass wir die Spitzen aller 12 Ecken abschneiden, würde die räumliche Figur aus 12 gleichseitigen Fünfecken und 20 gleichseitigen Sechsecken bestehen. Und wenn wir die Fünfecke nun schwarz einfärben und die Sechsecke weiß, dann gleicht das Ergebnis doch sehr dem, was wir suchen. Genau so ist nämlich der klassische Fußball aufgebaut – die Frage ist nur: Warum?
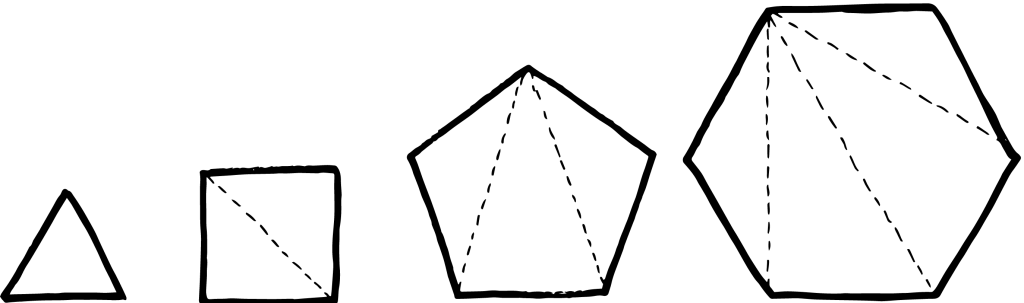
Die meisten erinnern sich aus ihrer Schulzeit vielleicht noch daran, dass die Summe der Winkel in einem Dreieck 180 Grad und in einem Viereck 360 Grad beträgt. Aber wie ist das bei einem Fünfeck und einem Sechseck? Wenn wir uns ein Dreieck ansehen, können wir für die Summe der Winkel im Dreieck einen klassischen mathematischen Beweis führen, aber wir können uns auch davon überzeugen, dass diese Aussage stimmt, indem wir eine Reihe von Untersuchungen an willkürlichen Dreiecken vornehmen. Den Beweis wollen wir hier jetzt nicht führen. Wir nehmen als Ausgangspunkt einfach an, dass die Summe der Winkel in einem Dreieck 180 Grad beträgt. Das können wir nutzen, um die Winkelsumme in einem Viereck, einem Fünfeck, einem Sechseck, ja, praktisch jeder beliebigen ebenen Figur zu bestimmen.
Wenn wir eine etwas rundere Form erreichen möchten, könnten wir versuchen, unseren Ball als Ikosaeder zu gestalten. So würde er aus 20 gleichseitigen Dreiecken bestehen, von denen jeweils 5 an 12 Ecken aufeinander treffen. Eine solche räumliche Figur würde, wie man auf dem Bild weiter oben gut erkennen kann, für einen runderen Ball sorgen, aber dieser Ball wäre nach wie vor ziemlich unberechenbar, da er immer noch in alle Richtungen springen und rollen könnte – je nachdem, wie er landet.
Wenn wir uns jetzt vorstellen, dass wir die Spitzen aller 12 Ecken abschneiden, würde die räumliche Figur aus 12 gleichseitigen Fünfecken und 20 gleichseitigen Sechsecken bestehen. Und wenn wir die Fünfecke nun schwarz einfärben und die Sechsecke weiß, dann gleicht das Ergebnis doch sehr dem, was wir suchen. Genau so ist nämlich der klassische Fußball aufgebaut – die Frage ist nur: Warum?
Die meisten erinnern sich aus ihrer Schulzeit vielleicht noch daran, dass die Summe der Winkel in einem Dreieck 180 Grad und in einem Viereck 360 Grad beträgt. Aber wie ist das bei einem Fünfeck und einem Sechseck? Wenn wir uns ein Dreieck ansehen, können wir für die Summe der Winkel im Dreieck einen klassischen mathematischen Beweis führen, aber wir können uns auch davon überzeugen, dass diese Aussage stimmt, indem wir eine Reihe von Untersuchungen an willkürlichen Dreiecken vornehmen. Den Beweis wollen wir hier jetzt nicht führen. Wir nehmen als Ausgangspunkt einfach an, dass die Summe der Winkel in einem Dreieck 180 Grad beträgt. Das können wir nutzen, um die Winkelsumme in einem Viereck, einem Fünfeck, einem Sechseck, ja, praktisch jeder beliebigen ebenen Figur zu bestimmen.
Dreieck: 180 grader/3 = 60 grader
Viereck: 360 Grad/4 = 90 Grad
Fünfeck: 540 Grad/5 = 108 Grad
Sechseck: 720 Grad/6 = 120 Grad
Betrachten wir die platonischen Körper, dann sind diese Winkelsummen wichtig für die Frage, wie rund ein Ball wird, den wir auf der Grundlage der platonischen Körper herstellen. Um eine räumliche Figur zu konstruieren, müssen wir an jeder Ecke mindestens 3 Figuren zusammensetzen. Setzen wir 4 Dreiecke zusammen, wie bei einem Tetraeder, beträgt die Winkelsumme in einer Ecke, in der 3 Dreiecke aufeinander stoßen, 3 x 60 = 180 Grad. Diese Ecke würden wir als sehr spitz wahrnehmen.
Setzen wir ein zusätzliches Dreieck ein, sodass nicht mehr nur 3, sondern 4 Dreiecke in einer Ecke aufeinander treffen, erreichen wir in der Ecke eine Winkelsumme von 4 x 60 = 240 Grad. Diese räumliche Figur hätte weniger spitze Ecken.
Wenn wir nun versuchen, in jeder Ecke ein 5. Dreieck einzusetzen, konstruieren wir einen Ikosaeder. Hier liegt die Winkelsumme der einzelnen Ecken bei 5 x 60 = 300 Grad. Im Vergleich zu einem Tetraeder und einem Oktaeder würden wir diese räumliche Figur wiederum als weniger spitz empfinden.
Setzen wir nun ein 6. Dreieck ein, würden wir herausfinden, warum wir aus Dreiecken nicht mehr als die drei genannten platonischen Körper konstruieren können. Denn hier würde die Winkelsumme in jeder Ecke 6 x 60 = 360 Grad betragen. Warum können wir auf diese Weise keine räumliche Figur erschaffen? „Denken, denken, denken …“
Die Ecke würde ganz flach ausfallen. Es würde uns nie gelingen, daraus eine räumliche Figur zu machen. Auf dieselbe Weise können wir auch für Quadrate, Pentagone und Hexagone begründen, weshalb immer nur die 5 genannten platonischen Körper konstruierbar sind. Probiere einmal aus, ob du dem Gedankengang hast folgen können.
Was ist nun aber mit der Winkelsumme in der Ecke des klassischen Fußballs? Jede einzelne Ecke eines Fußballs ist der Treffpunkt eines Fünfecks und zweier Sechsecke. Sieh dir das Bild des Fußballs an, um dich selbst davon zu überzeugen. So kommen wir in den Ecken auf eine Gesamtwinkelsumme von 108 + 120 + 120 = 348 Grad, was relativ nah an den 360 Grad ist, bei denen die Ecke flach wäre, aber doch weit genug davon entfernt, um einen räumlichen Körper zu erschaffen. Wie aus dem Modell hervorgeht, hat der räumliche Fußball nach mathematischem Verständnis immer noch scharfe Kanten, aber da er aus einem Material genäht wird, das ein wenig nachgibt, wie beispielsweise Leder, empfinden wir einen Fußball, der aus 12 gleichseitigen Fünfecken und 20 gleichseitigen Sechsecken besteht, als rund, wenn er aufgeblasen wird und sich das Material dehnt. Das ist der Grund dafür, dass der klassische schwarz-weiße Fußball so aussieht, wie er es nun einmal tut.
Tatsächlich können Fußbälle auch aus anderen platonischen Körpern konstruiert werden. Dies und andere lustige Fakten rund um Fußbälle findest du hier: https://www.youtube.com/watch?v=cwWBpjeyRS0. In diesem Video erläutert Matt Parker, ein australischer Mathematiklehrer und Stand-up-Comedian, die Geometrie hinter verschiedenen Fußbällen.
Mehr über die Geschichte des Balls kannst du auch hier nachlesen: https://web.archive.org/web/20150702050750/http:/www.selectsportamerica.com/history/
Illustrationen: Helle Lykke Østerby – November 2020

Gib den ersten Kommentar ab