Til Matematikugen i slutningen af maj er der produceret fem postkort med matematiske grublerier. Postkortene og deres indhold læser du mere om herunder.
Kravl igennem kortet – kan hullet i en ting være større end tingen selv?
Din umiddelbare indskydelse er måske: nej, det kan ikke lade sig gøre. Men det kan det faktisk!
Et lille hul i et todimensionelt fladt postkort kan udvides ved at man klipper i det og lader kortet bugte og krumme sig i tre dimensioner – og på den måde kan du selv kravle igennem et postkort.
Det er et tilsvarende overraskende faktum (for dem, der ikke kender det i forvejen) er, at en dansk 5-krone kan komme igennem et hul i et stykke papir på størrelse med en dansk 2-krone. Eller lidt mere matematisk formuleret, så kan en mønt komme igennem et hul i et stykke papir, der har en diameter, der er mindre end mønten selv.
Du kan helt praktisk tage et almindeligt stykke papir og tegne rundt om en dansk 1-krone og klippe langs stregen. Hullet i papiret bliver selvfølgelig lidt større end 1-kronen, men hullet har en mindre diameter end de andre danske kronemønter. Alligevel kan alle de større mønter komme igennem hullet uden der bliver klippet yderligere i papiret! Arh, tænker du … Det kan da ikke lade sig gøre.
Jo, den er go’ nok. Hvis du folder hullet på midten og trækker forsigtigt i “enderne” af hullet, så vrider papiret sig og med lidt forsigtig lirken, så kan selv den store 5-krone komme igennem hullet. I stedet for et cirkulært hul får du et aflangt smalt hul, som mønterne kan smutte igennem. Prøv selv efter!
Kan man gøre det samme med en 10 cent euro og så få de øvrige euromønter igennem hullet?
Hvis du trækker hullet i papiret helt ud, vil du teoretisk kunne få en længde på en halv gang omkredsen af hullet. Hvis vi sammenholder det med sammenhængen mellem omkreds og diameter i en cirkel: omkreds= π diameter, så får vi, at vi i teorien kan få en helt flad mønt – med en diameter π/2≈1,57 gange større end hullets diameter – lirket gennem hullet. I praksis vil det dog på grund af papirets stivhed være svært at komme tæt på dette teoretiske maksimum.
Det er også muligt at lave noget tilsvarende med ikke flade ting. Se mere her: Stand-up Maths – Can you make a hole in a thing bigger than the thing?: https://www.youtube.com/watch?v=gPIRLQZnRNk
Firfarveproblemet
Når man kigger i særligt gamle atlas, så er de forskellige lande farvet med forskellige farver. De er farvet sådan, at to lande, der har en fælles grænse, ikke har samme farve. I 1852 opdagede matematikeren Francis Guthrie, at han kunne farvelægge de engelske counties på denne måde, men ved kun at benytte fire forskellige farver. Så han stillede sig spørgsmålet om fire farver altid er nok til at farvelægge områder på et kort. Der skulle dog gå over hundrede år, før han kunne få et endeligt svar. Det blev først i 1970 matematisk bevist, at fire farver altid vil være tilstrækkeligt. Det er særligt at bemærke, at det er den første matematiske sætning, der er blevet bevist med hjælp fra en computer.
Numberphile med professor James Grimes: https://www.youtube.com/watch?v=NgbK43jB4rQ
Monty Hall
Nogle gange bliver vi snydt af vores matematiske intuition. Særligt, når sagen drejer sig om sandsynligheder, kan det være en udfordring. Et klassisk eksempel på dette stammer fra et amerikansk quizshow, hvor værten for showet hed Monty Hall, hvilket er årsagen til, at problemet kaldes for Monty Hall-problemet. Læs og se mere via disse to links:
Dansk: https://da.wikipedia.org/wiki/Monty_Hall-problemet
Tysk: https://de.wikipedia.org/wiki/Ziegenproblem
Numberphile med Lisa Goldberg: https://www.youtube.com/watch?v=4Lb-6rxZxx0
En-stregstegninger
Nogle stregtegninger kan tegnes i en lang streg uden at løfte blyanten – andre kan ikke. Den gren af matematikken, der kaldes graf-teori kan hjælpe dig med at svare på, hvilke der er mulige at tegne i én streg, og hvilke der kræver mere end en streg. Læs hvordan i disse to MatOnline-artikler:
Dansk: https://www.matkult.eu/matonline/index.php/2019/matematiske-puslerier-med-streger/
Tysk: https://www.matkult.eu/matonline/index.php/de/2019/die-mathematik-hilft-graphentheorie/
Dansk: https://www.matkult.eu/matonline/index.php/2020/matematiske-puslerier-med-streger-ii/
Tysk: https://www.matkult.eu/matonline/index.php/de/2020/mathematische-ratsel-mit-linien-ii/
Findes der matematikopgaver, hvor alle svar er rigtige?
Mange har den opfattelse, at matematikopgaver skal have ét rigtigt svar – og at det netop er det, matematik går ud på: at bruge den rigtige metode til at finde det korrekte svar, og helst hurtigt.
Men sådan er det ikke! Ikke kun i hvert fald.
Gode og interessante matematikopgaver kan ofte besvares på mange forskellige måder, og der kan sagtens være mere end ét korrekt svar.
Lad os vende tilbage til spørgsmålet i overskriften. Findes der matematikopgaver, hvor alle svar er rigtige? Ja! Det gør der. I har tidligere på MatOnline.dk i artiklen Hvilken hører ikke til? kunnet læse om den type opgaver. Her kommer der nogle flere, og en opfordring til selv at konstruere sådanne opgaver.
Denne opgavetype består af fire objekter. Det kan fx være tal, figurer, billeder eller grafer. Kun fantasien sætter grænser. Spørgsmålet i opgaverne er altid det samme: Hvilken af de fire passer ikke ind?
Her er vist en ”Hvilken passer ikke ind?”-opgave. Den er lavet ud fra fire kort fra kortspillet SET. Du kan læse om spillet SET her. Prøv om du kan komme med nogle bud på svar.
- Kortet øverst til venstre stikker ud, for det er grønt, og de tre andre er røde.
- Joh, men man kan også sige at kortet øverst til højre ikke hører til, for det har ruder-figurer, mens de tre andre har slange-figurer.
- Men kortet nederst til venstre har tre figurer, mens de andre kun har to, så det skiller sig ud.
- Det sidste kort nederst til højre skiller sig ud, for der er farven ikke fyldt ud.
Konklusionen er, at hvert af kortene på hver sin måde ikke passer ind. Altså er alle svar korrekte. Det, der er det udfordrende, er at kunne argumentere for, hvorfor det enkelte kort skiller sig ud.
Lad os prøve en opgave mere. Denne gang er den lavet ud fra fire almindelige spillekort. Måske er den lidt sværere, men prøv alligevel, om du kan komme med en forklaring:
- Hvorfor passer spar 4 ikke ind?
- Hvorfor passer ruder 5 ikke ind?
- Hvorfor passer damen ikke ind?
- Hvorfor passer hjerter 8 ikke ind?
Det kan måske hjælpe at tænke over egenskaber ved tallene og ved figurerne på kortene.
Du kan også få en kammerat til at kigge på kortene. Det er ikke sikkert, at I får øje på de samme ting – og det er heller ikke vigtigt. Det vigtige er at kunne argumentere for, hvorfor man mener, at et bestemt kort ikke passer ind.
De argumenter, jeg tænkte på, da jeg konstruerede opgaven, er:
- Spar 4 er sort
- 5 er et ulige tal
- Damen er det eneste billedkort
- Hjerter 8 er det eneste kort, hvor man kan se hvis kortet drejes 180 grader. De tre andre har rotationssymmetri
Måske du har fundet på andre argumenter – det vil bare være fantastisk, for så er der endnu flere måder at løse opgaven på, og der er grundlag for gode samtaler om egenskaberne ved kortene i opgaven.
Denne type opgave er designet af Christopher Danielson netop til at stimulere vores nysgerrighed og give anledning til gode samtaler om matematiske egenskaber. Han er forfatter til billedbogen ”Which One Doesn’t Belong?” til børn, der indeholder figuropgaver af typen ”Hvilken passer ikke ind?”.
Her til sidst kommer der to opgaver mere, som er hentet fra siden https://wodb.ca/ – WODB står for Which One Doesn’t Belong. På siden er der en stor samling af ”Hvilken passer ikke ind?”-opgaver
En med fire tal, og en er med trekanter, der er inddelt på forskellige måder.
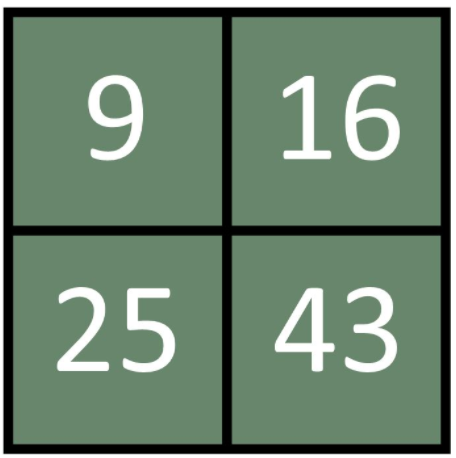
Her kan man fx komme på disse argumenter:
Talopgaven
- 9 er et ciffer, som ikke har tværsummen 7
- 16 er et lige tal. 4 går op i tallet
- 25 er summen af to af de andre tal. Tallet går op i 100
- 43 er et primtal. Tallet er ikke et kvadrattal
Trekantopgaven
- Øverst til venstre: Den eneste figur, som består af forskellige indre figurer. Den eneste figur, hvor de indre figurer ikke er kongruente. Den eneste figur, der ikke har rotationssymmetri
- Øverst til højre: Den eneste figur med fire indre figurer. Den eneste figur, hvor de indre figurer har samme form som selve figuren. Den eneste figur, hvor alle vinkler er lige store (60 grader)
- Nederst til venstre: Den eneste figur, der indeholder rette vinkler. Den eneste trekant, der står på spidsen
- Nederst til højre: Den eneste figur, der har konkave indre figurer. Den eneste figur med vinkler på mere end 180 grader. Den eneste figur, der ikke har spejlingssymmetri
Prøv selv om du kan konstruere nogle WODB-opgaver.
Denne type opgaver er også beskrevet i denne MatOnline-artikel:
Dansk: https://www.matkult.eu/matonline/index.php/2022/hvilken-hoerer-ikke-til/
Tysk: https://www.matkult.eu/matonline/index.php/de/2022/hvilken-hoerer-ikke-til-2/
Start debatten med en kommentar