Vi har tidligere skrevet om Uwe Seelers fod og om en fodbold er rund. Der er i fodbold over de seneste år blevet et større fokus på forventede mål (xG), der opstiller en model for måling af ’kvaliteten’ af en afslutning og derved forsøger at belyse sandsynligheden for at der scores eller forventes at scores mål. Afslutninger er defineret ud fra en skala fra 0 til 100 % chance for mål pr chance. I grove træk, så vil en chance tættere på mål resultere i en højere xG værdi:
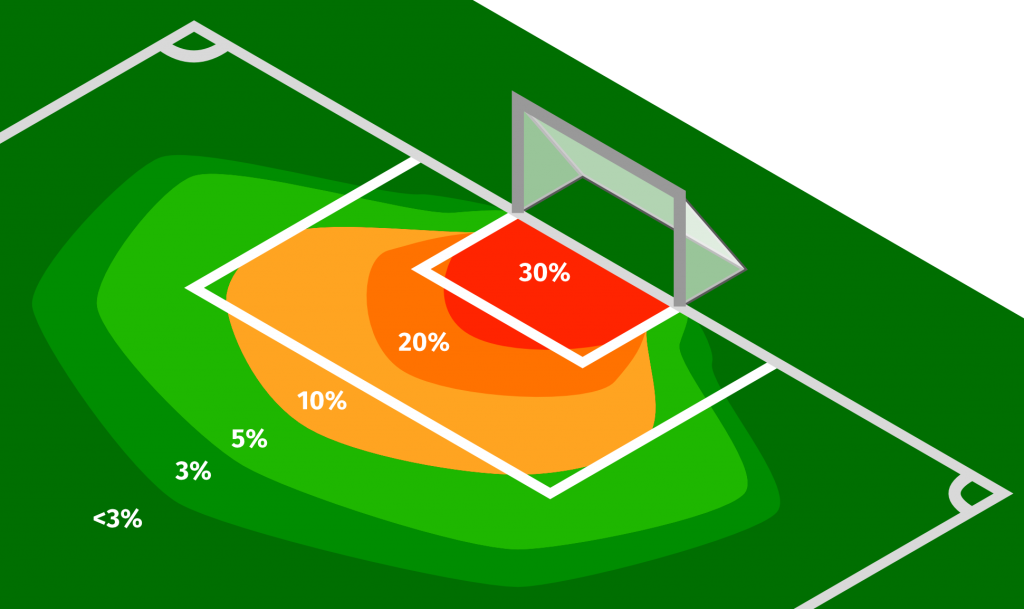
Det er nærmest en form for varmekort over, hvor muligheden for mål er størst.
Derudover, fokuseres der meget på den enkelte spiller, holdets evne til at score (set over tidligere kampe), osv. Man har mange parametre, man kan måle på og tage i betragtning, når man skal lave en xG model, og grundlæggende forsøger den at belyse situationers evne til at resultere i mål. Det er også derfor, de ikke altid rammer plet, da det er vigtigt at gøre opmærksom på, at xG primært forsøger at give en idé om størrelsen på de chancer, der opstår. Der er faldgruber, når man skal lave en model, og i xG kan der være situationer, såsom straffespark, hjørne eller frispark, hvor målvogteren kan redde bolden og en efterfølgende løs bold kan resultere i en ny chance. I virkeligheden er der kun mulighed for 1 mål pr. situation, da spillet genstartes fra midten ved mål, f.eks. kan følgende situation opstå:
Straffespark: 0,80 forventet mål
Efterfølgende chance: 0,70 forventet mål
Resultat: 1,50 forventet mål
Så en model skal tage stilling til, ‘hvornår’ en situation er slut, da man ikke ukritisk kan lægge procenter sammen. Ellers vil ovenstående problemstilling kunne opstå, hvor vi tager hvert skud som én chance for mål, men i virkeligheden hænger de to situationer sammen. Du kan læse mere om den problematik her og hvordan xG tager det med ved at tilføje et ekstra trin:
The maths behind this particular situation is as follows.
— The xG Philosophy (@xGPhilosophy) July 21, 2020
(1 - 0.78) x (1 - 0.90) = n
0.22 x 0.10 = 0.02
So there’s a 2% probability that Man City don’t score either chance.
Therefore:
1 - 0.02 = 0.98(xG)
So Man City should be awarded 0.98(xG) for this attack.
(5/6)
Kort fortalt, så vil xG i eksemplet ovenfor være 0,94 forventet mål og ikke 1,50 forventet mål:
Straffespark + (1 – Straffespark) · Efterfølgende chance =
0,80 + (1 – 0,80) · 0,70 = 0,94 forventet mål for situationen
Den tager hver enkelt chance og forsøger at kvantificere den ud fra, hvor chancen opstår, vinklen til målet, hvem der sparker, hvor mange mål de tidligere har scoret, hvor mange kampe de har spillet og mange flere ting. Som du kan se mere om her: https://oneshortcorner.wordpress.com/2016/03/06/football-analytics-part-four-expected-goals/
Modeller for Expected goals
Det er ikke klart, hvad de enkelte modeller indeholder, men vi kan forsøge at lave vores egen. Vores model vil dog være simplificeret og tage udgangspunkt i én situation og ikke en kamp:
Lionel Messi får bolden lige uden for feltet og dribler forbi en modspiller og ind i feltet og skyder!
Men scorer han?
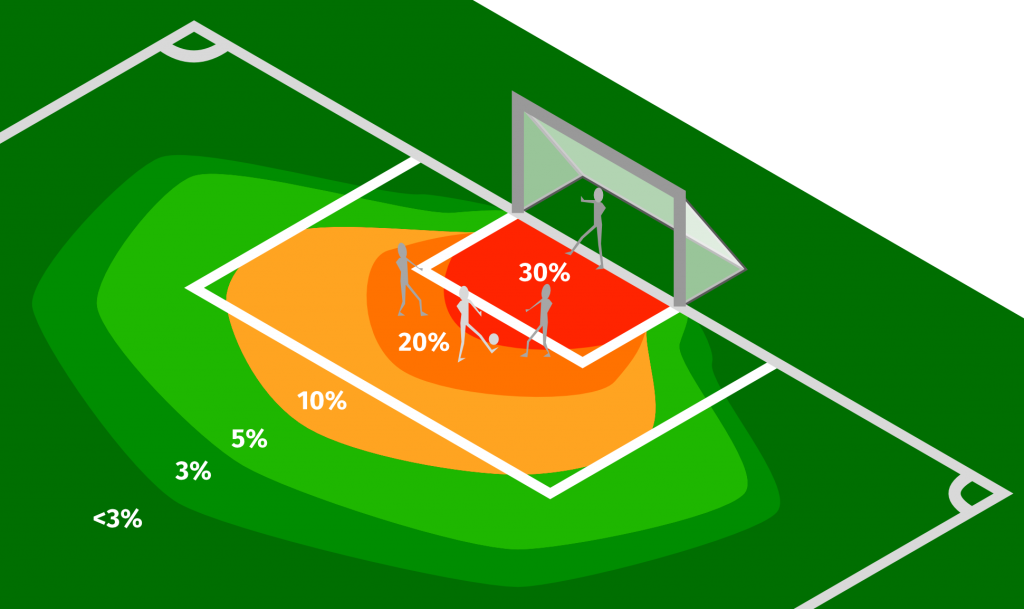
Lad os se på en simpel forventet-mål-model, hvor vi kigger på et par faktorer:
[(Stedet, hvor afslutningen finder sted) + (Vinklen mod mål)] · [(Spillerens forventede mål pr kamp/pr chance) · (Mål pr skud på mål af holdet)] – [Målmand – forsvaret] · (faktor af hvor mange mål holdet forventer at indkasserer/pr skud på mål) =
(0,30 + 0,20) · (0,028 [jf. 1,4 mål/50 skud på mål, OneShortCorner] · 25)
– (0,1 – 0,1) · 0,95 = 0,35 forventet mål
Så i vores model, vil vi forvente mål i over en tredjedel af gangene, denne situation opstår. Der ligger meget data bagved en ’rigtig’ xG model, hvor statistik – såsom hvor mange mål Messi scorer pr 50 skud – ligger til grund for, hvordan enkelte situationer måles. Denne model er simpel, men har du lyst til at prøve kræfter med at lave en ‘rigtig’ xG-model med flere elementer, så kig med på denne YouTube-video i tre dele: https://www.youtube.com/watch?v=bpjLyFyLlXs
Vi kan hurtigt udvide vores model ved at kigge på om et hold scorer mere på hjemmebane end på udebane, dommeren, hvor mange kort en nærliggende modstander har og mange flere faktorer.
Der skal overvejes, hvornår en situation slutter, så vi har en konkret xG-værdi for hver chance i en kamp. Generelt set, kigger xG på det pr skud – dog skal der yderligere beregning til, såfremt der kort tid efter sker endnu en chance, såsom med eksemplet med straffesparket fra tidligere. Så en xG-værdi kan ændre sig i et tidsrum efterfølgende og de enkelte situationer er meget nemmere at beregne end en hel kamp fyldt med en masse uforudsigeligheder, 22 spillere, 3-5 dommere, 2 trænere og tilskuere. Som du kan se, så kan modellen hurtig blive meget kompleks.
xG kan bruges til mange ting, men bliver ofte brugt internt på hold til at analysere, hvor holdet og den enkelte er bedst til at score, hvordan chancer opstår og hvornår de opstår. Spørgsmålet er om man overhovedet kan forudsige antallet af mål.
Du kan læse mere om Expected goals her:
https://towardsdatascience.com/a-guide-to-expected-goals-63925ee71064

Start debatten med en kommentar