I disse tider er medierne fyldt med matematiske modeller. De matematiske modeller danner baggrund for de beslutninger, som myndigheder og politikere træffer grundet udviklingen af COVID-19 pandemien, men hvordan gør de egentlig det? Dette vil du måske blive lidt klogere på ved at læse denne artikel. Du vil IKKE kunne bruge eksemplerne og modellerne i artiklen til at forudsige den præcise udvikling af COVID-19 pandemien, da eksemplerne kun i nogen grad tager udgangspunkt i virkeligheden og modellerne i artiklen er meget mere simple end dem myndighederne anvender. Du kan måske til gengæld bliver klogere på, hvordan myndighederne grundlæggende bruger matematisk modellering til at forudsige udviklingen i antallet af smittede under en pandemi som denne.
Hvad er matematisk modellering?
En matematisk model er en matematisk beskrivelse af sammenhænge bestående af formler, ligninger, matematiske udtryk eller lignende, som kan anvendes til at lave beregninger på og forudsigelser af en problemstilling fra virkeligheden. Matematisk modellering er i forlængelse heraf arbejdet med at opstille og anvende en sådan matematisk model. Dette arbejde kan lidt forsimplet inddeles i tre delprocesser, som er repræsenteret ved pilene i figuren herunder.
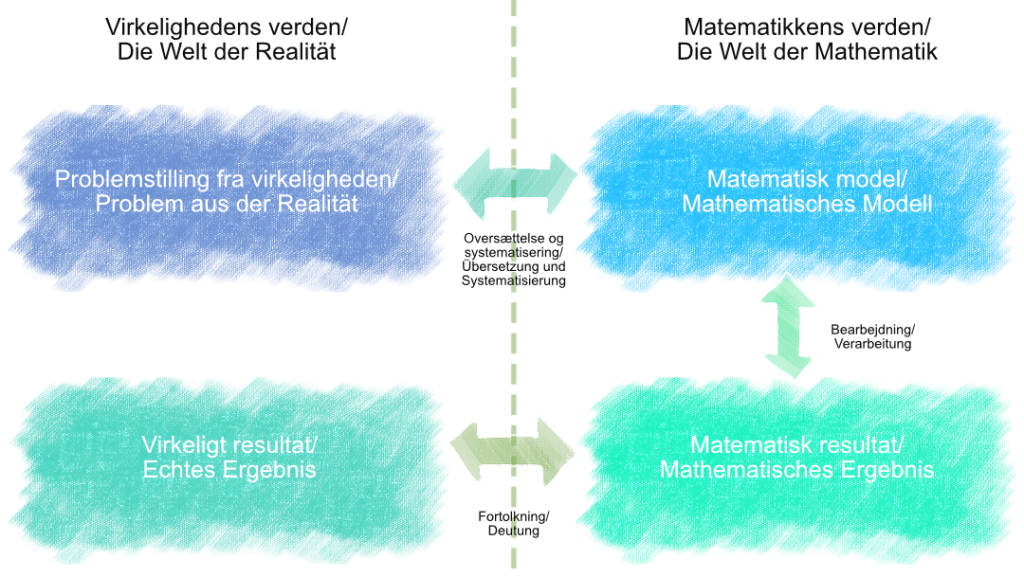
Den mørkeblå pil i modellen er første delproces. Her handler det om at systematisere og oversætte en problemstilling eller en situation fra virkeligheden til en matematisk model. I problemstillingen fra denne artikel vil udgangspunktet være, at undersøge hvilke parametre der kan have betydning for den forventede smittespredning af coronavirus. Virkeligheden er ofte meget kompleks at lave beregninger på, hvorfor der i denne del af processen skal tages en masse valg og fravalg for at forenkle en ellers kompleks virkelighed. I denne delproces vil udkommet være et system af parametre, som skal oversættes til matematik og opstilles i en matematisk model, som kan anvendes i den næste delproces.
I den næste delproces – den turkise pil i modellen – kan den opstillede matematiske model bruges til at lave matematiske beregninger på virkeligheden med udgangspunkt i konkrete tal gennem en matematisk bearbejdning.
I den tredje og sidste del af processen – den grønne pil – skal den matematiske beregning fortolkes tilbage til et resultat i virkelighedens verden. Efterfølgende kan det være nødvendigt, at se tilbage på processen og ændre i systematiseringen og/eller den matematiske model for at få et mere præcis resultat.
I situationen med COVID-19 pandemien bliver den matematiske model løbende korrigeret i gentagne modelleringsprocesser. Vi bliver hele tiden klogere på, hvordan de indgående variable påvirker hinanden – hvor smitsom virus er, hvordan befolkningen opfører sig, hvor effektive forskellige til tag er, Osv. Jo bedre vi forstår problemet, jo bedre kan vi beskrive det matematisk. Præcis på samme gælder for meteorologers vejrudsigter; jo mere præcise vejrdata og jo bedre forståelse af vejrfænomener, jo mere præcise kan vejrudsigterne blive.
Hvorfor er smittetrykket vigtigt?
En af de mange modeller der har været gengivet i både tyske og danske medier, særligt i løbet af marts i starten af pandemiens udvikling, var ”den stejle” og ”den flade” kurve. Kurverne beskrev to mulige scenarier for, hvordan smitten ville udvikle sig. Hvordan, den faktiske kurve kom til at se ud, ville blandt andet afhænge af smittetrykket.
Smittetrykket fortæller os, hvor mange andre en syg person gennemsnitligt vil smitte i løbet af et sygdomsforløb. Er smittetrykket 2 betyder det, at en syg gennemsnitligt smitter 2 nye personer i løbet af hele sygdomsforløbet. De 2 nye smittede bliver syge og vil også smitte 2 nye personer hver. Dette giver i alt 2 x 2 = 4 nye smittede i tredje led, som igen bliver syge og smitter videre i en smittekæde. Antallet af smittede vil i dette tilfælde stige drastisk gennem relativt få led. Dette kaldes i matematikken for eksponentiel vækst.
Hvis smittetrykket ligger på 2 og en syg smitter videre indenfor fem dage, så skal vi her se nærmere på, hvor mange smittede et smittet kærestepar kan være årsag til efter blot 30 dage.
Kæresteparret er blevet smittet af en ukendt kilde og har ikke umiddelbart nogen symptomer. Derfor tager de ubekymret i biografen. På vej til biografen smitter en af dem først en medpassager i bussen, så bliver hende der tjekker deres billetter i biografen smittet, herefter en af de personer, som sidder ved siden af dem i biografen og på vej til bussen hjem møder de en ven, som også smittes. De går hjem i seng, vågner op med feber og bliver hjemme til de er raske igen. Efter biografturen er der nu 4 personer mere, som er blevet smittet. Dette svarer til et smittetryk på 2, da en syg har resulteret i gennemsnitlig 2 nye smittede og 2 syge derfor har resulteret i 4 nye smittede. De 4 nye smittede fra kæresteparrets biograftur bliver syge og smitter videre i kæden og udviklingen efter 30 dage vil se sådan ud for antallet af nye smittede, da dette antal fordobles for hvert led:

Et smittetryk på 2 vil samlet have medført, at der efter 30 dage vil være kommet 128 nye smittede i syvende led i en kæde der startede med kun 2 smittede. De 128 kan smitte videre i en eksponentielt voksende smittekæde, hvis smittetrykket ikke sænkes.
Myndighederne er interesseret i at mindske smittetrykket. Dette både for at beskytte de ældre og særligt udsatte, men også for at der er kapacitet nok på sygehusene til at hjælpe dem, som har brug for det. Dette har medført at mange lande i en periode har lukket samfundet helt eller delvist ned, og generelt er der en anbefaling om at holde fysisk afstand og flere tiltag omkring øget hygiejne. Med en nedlukning vil kontaktniveauet mindsket. Dette betyder at en syg vil smitte færre nye, da han eller hun simpelthen vil være i kontakt med færre mennesker. Smittetrykket er altså blandt andet afhængigt af kontaktniveauet i samfundet. Beregninger på det forventede kontaktniveau og smittetryk ved forskellige tiltag indgår som en vigtig del af myndighedernes systematisering til at opstille en model til beregninger af udviklingen i antallet af smittede.
Hvis vi forestiller os, at en smittet person nu ikke længere gennemsnitligt spreder smitten til 2 personer, men kun til 1,5 grundet diverse tiltag, så lyder en ændring på gennemsnitligt 0,5 person mindre pr. smittet måske ikke af så meget, men på en eksponentiel kurve, så vil det hurtigt få stor betydning for antallet af smittede.
Med udgangspunkt i eksemplet med kæresteparret fra før, så vælger de nu at tage egen bil til biografen i stedet for bussen. Deres kontaktniveau bliver derfor mindsket og dermed også smittetrykket. Da de ikke tager bussen smitter de ikke medpassageren. De smitter til gengæld stadig hende der tjekker billetter og en af de andre biografgæster. Selvom de tager bilen hjem møder de stadig vennen, som også smittes. Derfor har de nu i stedet for 4 kun smittet 3 nye personer, men hvilken betydning får det egentlig på den lange bane? Udviklingen vil på 30 dage se ud som følgende med et smittetryk på 1,5:

Der kan selvfølgelig ikke være 4,5 nye smittede personer i tredje led i virkeligheden, da halvdelen af et menneske ikke kan være smittet uden at den anden halvdel også er det, men da der regnes ud fra et gennemsnit, så vil denne matematiske beregning resultere i decimaltal, når der som her ganges med 1,5 for hvert led. Med et smittetryk på 1,5 vil der efter de 30 dage være 22,8 nye smittede, som vi kan fortolke over i virkeligheden til ca. 23 nye smittede i syvende led. Dette er ca.105 mindre end ved smittetrykket på 2, hvor der i syvende led var 128 nye smittede. Derfor vil belastningen på sygehusene blive markant mindre ved at mindske smittetrykket selv en lille smule. En sammenligning af forskellen på udviklingen i antallet af nysmittede for hver 5 dag kan ses i grafen med de to kurver herunder.
Hvis smittetrykket kommer under 1 vil færre og færre blive smittet, og antallet af syge vil gradvist falde. Dette kan ske ved tiltag som social distance og bedre hygiejne, samt ved udvikling af flokimmunitet.
Et smittetryk på 2 over for et smittetryk på 1,5 gav en forskel på ca.105 nye smittede efter 30 dage med sygdommen og dette med udgangspunkt i kun 2 smittede på dag 0. Havde vi i stedet set på 60 dage med smittetryk på hhv. 2 og 1,5, så ville forskellen have været langt større. Efter 60 dage ville de 2 syge ved et smittetryk på 2 have resulteret i 8.192 nye smittede i 13. led (dag 60) og kun 259 nye smittede ved et smittetryk på 1,5. Altså en ikke uvæsentlig forskel på 7.933 smittede 60 dage efter kæresteparret tog i biografen. Alt dette på grund af forskellen i den eksponentielle vækst i udviklingen af antal smittede. Havde smittetrykket været lidt højere eks. 2,5, så ville der efter 60 dage være 119.209 nye smittede i 13. led. Derfor er myndigheder og politikere meget optaget af, at få viden om og sænke smittetrykket, så kapaciteten i sundhedsvæsnet ikke overskrides.
”Den stejle” og ”den flade kurve”
Det antages at sygdommen kan stoppes på to måder. Begge dele kræver, at smittetrykket falder gradvist indtil det når 0. Smittetrykket og dermed sygdommen kan stoppes på grund af tiltag som social afstand, forbedret hygiejne, samt smitteopsporing og karantæne. Dette kræver dog en gennemgribende, systematisk og langstrakt indsats. Den anden måde er ved flokimmunitet, som betyder at en stor nok del af befolkningen har været smittet og har udviklet immunitet, at sygdommen får svært ved at sprede sig, da de immune ikke længere kan sprede sygdommen. De, som ikke har været smittet, vil derfor ikke komme til at møde ret mange, som de kan smittes af. Smittetrykket falder derfor og sygdommen stopper med tiden helt med at sprede sig. Flokimmunitet kan også opnås gennem vaccine, som dog for COVID-19 endnu ikke er udviklet.
Vi antager at 60% (vurderes pt i Danmark til at være 60-70% under corona-pandemien) af en befolkningsgruppe skal smittes med eller vaccineres for en given sygdom for at opnå flokimmunitet. I et land med 1.000.000 indbyggere skal 600.000 (60%) indbyggere altså have haft sygdommen, hvis en vaccine ikke er tilgængelig, før end der opnås flokimmunitet. Hvis de 600.000 personer smittes inden for en meget kort periode, så vil landets sygehusvæsen ikke kunne følge med. Dette scenarie er ”den stejle kurve”, som er udtryk for et højt smittetryk. Hvis vi i stedet sænker smittetrykket, vil der stadig være 600.000, som skal have sygdommen, for at opnå flokimmunitet, men de vil få den over en meget længere periode, som ikke belaster sygehusvæsenet i samme grad, da der er færre syge på samme tid. Dette er ”den flade kurve”.. Der hersker dog tvivl, om det vil være muligt at opnå flokimmunitet i forbindelse med COVID-19 pandemien.
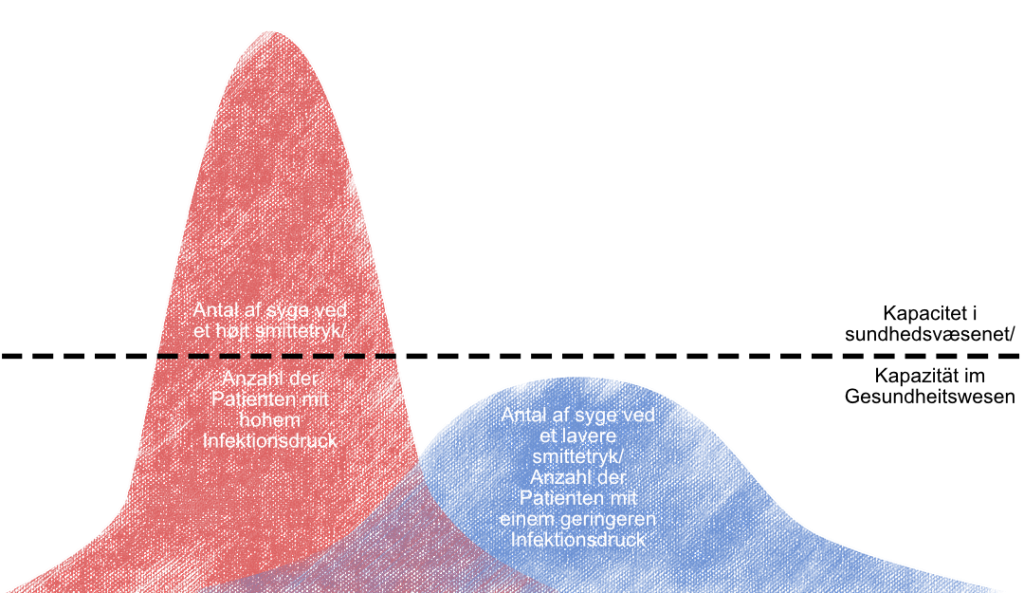
Hvis vi skal have viden om et lands sygehusvæsen kan følge med antallet af syge, så er det dog nødvendigt at se på langt flere parametre end blot kontaktniveau og smittetryk. Derudover er kontaktniveau og smittetryk forskellig for forskellige befolkningsgrupper. De yngste vuggestuebørn har formentligt et langt mindre kontaktniveau end for eksempel deres forældre. De unge har formentlig et højere kontaktniveau end de ældste. Nogle aldersgrupper smitter måske generelt mere end andre osv. Der ud over så er der også mange andre parametre som vi må tage højde for, hvis vi skal lave en brugbar matematisk model, som kan fortælle os noget om udviklingen i antallet af smittede, herunder eks. inkubationstid, længden på sygdomsforløb, hvor længe en syg smitter mm.
Når landene åbner mere og mere op igen, så vil der sidde eksperter, som anvender matematiske modeller til at beregne mulige ændringer i kontaktniveauet og smittetryk. Beregningerne vil bygge på kvalificerede gæt, men de vil også være fulde af usikkerheder. En matematisk model kan aldrig blive mere præcis, end de data og viden den bygger på. Så om de får ret i deres forudsigelser, det vil vi først vide, når vi er på den anden side af pandemien.
Pas godt på jer selv og hinanden – på afstand.
Du kan læse mere om modellerne bag de danske myndigheders beregninger her:
https://www.ssi.dk/aktuelt/sygdomsudbrud/coronavirus
“Modelberegninger for scenarier ved genåbning af Danmark”
Det kan give et indblik i hvordan scenarier og forudsigelser ændrer sig fra start april til her slut maj – i stil med hvordan vejrudsigten også ændrer sig fra dag til dag efterhånden, som meterologerne bliver klogere.

Start debatten med en kommentar